Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 2b

Calcule o volume do sólido W descrito abaixo:

(b) W é limitado pelas superfícies z = 8 - x 2 - y 2 e z = x 2 + 3 y 2 .

Passo 1

Aobaa, Firme?? Prontasso pra matar mais uma questãozinha?!

Vamo tentar esboçar essas superfícies pra ver se identificamos muito bem que é o nosso sólido. Repara que se tratam de dois parabolóides, um voltado pra cima com vértice na origem e o outro voltado pra baixo com vértice em z = 8 ; olha só como fica:

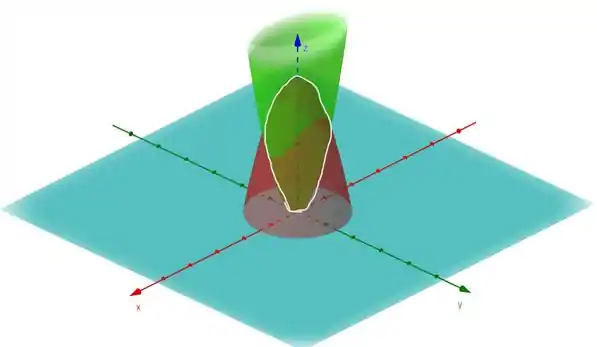
Então repare que o nosso sólido é limitado superiormente pelo parabolóide z = 8 - x 2 - y 2 , e limitado inferiormente pelo parabolóide z = x 2 + 3 y 2 .

Podemos utilizar alguma mudança de variáveis para calcular o volume, basta ver como a projeção desse sólido se comporta no plano x y .

Então tomando a intersecção dos dois parabolóides:

8 - x 2 - y 2 = x 2 + 3 y 2

Teremos:

2 x 2 + 4 y 2 = 8

Ou então:

x 2 4 + y 2 2 = 1

Lembra o que isso representa??? Um circulo talvez...?? Quaaasseee isso... Na verdade é uma elipse! Olha só:

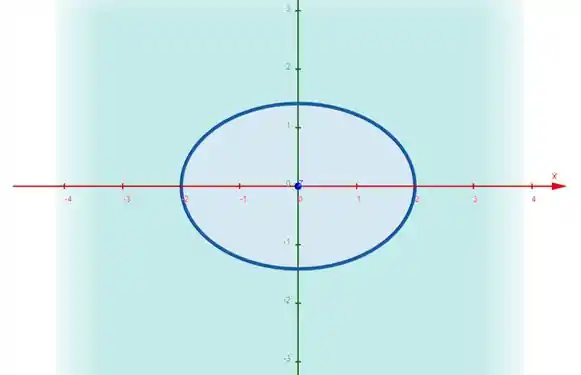
Olhando esse sólido de cima, é isso que a gente vê. Uma elipse que corta nos pontos 4 = ± 2 no eixo x . E 2 = ± 1,41 no eixo y .

Bom, então podemos utilizar coordenadas elípticas.

Passo 2

Show dibola então vamos ver os limites de integração:

Repara o seguinte:

x 2 4 = x 2 = r cos ⁡ θ → x = 2 r cos ⁡ θ y 2 2 = y 2 = r sin ⁡ θ → y = 2   r sin ⁡ θ

Lembra? Sempre que tínhamos um circulo fazíamos:

x = r   c o s θ       e       y = r   s i n θ

Mas desta vez temos uma elipse, mas a ideia é praticamente a mesma.

Bom, como a elipse esta nos 4 quadrantes do plano x y já sabemos que:

0 ≤ θ ≤ 2 π

Beleza, mas e o r ? Se você se lembrar, sempre teremos:

0 ≤ r ≤ 1

Quando fazemos essa transformação para elipses.

Agora, falta o z ainda né?! Vamos olhar pro nosso sólido; se nos estivermos em algum ponto no plano x y dentro da elipse, e resolvermos subir pra cima (ah vá) no sentido de z . A primeira superfície que vamos bater de frente é o parabolóide voltado pra cima e se continuarmos subindo, em um outro momento vamos dar de cara com o parabolóide voltado pra baixo. O que isso significa:

x 2 + 3 y 2 ≤ z ≤ 8 - x 2 - y 2

Pegou a idéia??

Mas nosso x já não é mais x , precisamos então mudar essas superfícies para as coordenadas que estamos usando:

z = x 2 + 3 y 2 = 4 r 2 cos 2 ⁡ θ + 6   r 2 sin 2 ⁡ θ = 6 r 2 - 2 r 2 cos 2 ⁡ θ

Mas, sin 2 ⁡ θ = 1 - cos 2 ⁡ θ , então:

z = 6 r 2 - 2 r 2 cos 2 ⁡ θ

E mesma idéa para o outro parabolóide:

z = 8 - x 2 - y 2 = 8 - 4 r 2 cos 2 ⁡ θ - 2 r 2 sin 2 ⁡ θ

Mudando o seno:

z = 8 - 2 r 2 - 2 r 2 cos 2 ⁡ θ  

Com isso, temos os três limites de integração. Mas to sentindo que ainda falta alguma coisa....

Como pudemos esquecer do Tio Jaco?? Precisamos dele lembra??

Em se tratanto de coordenadas elípticas, o jacobiano será:

J = a b   r

Então no nosso caso:

J = 2 2   r

Agora sim...

Passo 3

O volume dessa criatura será:

V = ∫ 0 2 π ∫ 0 1 ∫ 6 r 2 - 2 r 2 cos 2 ⁡ θ 8 - 2 r 2 - 2 r 2 cos 2 ⁡ θ 2 2   r   d z   d r   d θ

Cair matando em cima disso, bora:

V = ∫ 0 2 π ∫ 0 1 2 2 r 8 - 2 r 2 - 2 r 2 cos 2 ⁡ θ - 6 r 2 - 2 r 2 cos 2 ⁡ θ   d r   d θ

Caraca mlk, que dia, que isso... Carmeia! muito cuidado com os sinais, e foco. Little Thiago está conosco.

Isso nos dará:

V = ∫ 0 2 π ∫ 0 1 2 2   r 8 - 8 r 2   d r   d θ  

A próxima:

V = ∫ 0 2 π ∫ 0 1 2 2 8 r   d r - 8 r 3   d r   d θ  

V = 2 2 ∫ 0 2 π 8 r 2 2 - 8 r 4 4 d θ   r = 1 r = 0

Teremos:

V = 2 2 ∫ 0 2 π 4 - 2 d θ

Por último:

V = 2 2   2 θ θ = 2 π θ = 0

Finalmente:

V = 8 π 2

Ufa! Deu pra cansar!

Resposta

Concluindo,

V = 8 π 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os volumes das regiões nos Exercícios 23-36.A região entre o cilindro z = y 2 e o plano x y que é delimitada pelos planos x = 0 , x = 1 , y = - 1 , y = 1
Encontre os volumes das regiões nos Exercícios 23-36.A região cortada do cilindro x2 + y2 = 4 pelo plano z = 0 e oplano x + z = 3
Nos Exercícios 37-40, encontre o valor médio de F(x, y, z) sobre aregião determinadaF(x, y, z) = x2 + y2 + z2 sobre o cubo no primeiro octante, delimitado pelos planos coordenados e os planos x = 1, y
Encontre os volumes das regiões nos Exercícios 23-36.A região cortada do cilindro elíptico sólido x2 + 4y2 ≤ 4 peloplano xy e o plano z = x + 2.
Encontre os volumes das regiões nos Exercícios 23-36.A região no primeiro octante delimitada pelos planos coordenados, o plano y + z = 2 e o cilindro x = 4 - y 2