Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.8 - Ex. 88
Certo ou errado? Justifique em poucas palavras.
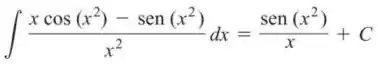
Passo 1
Para verificarmos se a fórmula dada está correta pode-se realizar a operação inversa à integração, ou seja, derivar a função do lado direito da equação. Fazendo isso, será encontrada a expressão que deveria estar dentro da integral no lado esquerdo da equação.
Passo 2
Portanto,
Passo 3
Esse último resultado mosta que a expressão que deveria estar sendo integrada é :
Resposta
A fórmula está errada.
Exercícios de Livros Relacionados
Uma partícula desloca-se sobre o eixo x com velocidade v t = t + 3,t ≥ 0 . Sabe-se que, no instante t = 0 , a partícula encontra-se na posição x = 2 .a) Qual a posição da partícula no instante t ?b) D
5.Determine a função y = y x ,x ∈ R , tal quef) d y d x = e - x e y 0 = 1
5. Determine a função y = y x ,x ∈ R , tal quec) d y d x = cos x e y 0 = 0
5. Determine a função y = y x ,x ∈ R , tal quee) d y d x = 1 2 x + 3 e y - 1 = 0
Uma partícula desloca-se sobre o eixo x com função de posição x = x t ,t ≥ 0 . Determine x = x t , sabendo que d 2 x d t 2 = 3 , v 0 = 1 e x 0 = 1