Se uma circunferência de raio rola ao longo do interior da circunferência , um ponto fixo de descreve uma curva chamada epicicloide, com equações paramétricas . Faça o gráfico da epicicloide e use (5) para calcular a área da região que ela envolve.
Passo 1
Fala, pessoal! Tranquilo?
A questão pede o gráfico da epicicloide com equações paramétricas:
Para isso podemos usar softwares gráficos como o GeoGebra.
E pede a área da região dentro dessa figura usando a equação 5 do nosso livro, que é:
Aqui usaremos:
Então, como o próprio enunciado nos dá a parametrização do epicicloide, vamos encontrar os limites de integração da integral acima e calculá-la normalmente.
Vamos chamar a curva descrita no enunciado de , traçando o gráfico temos
Vamos resolver!
Passo 2
Colocando as equações paramétricas numa calculadora gráfica:
Temos:
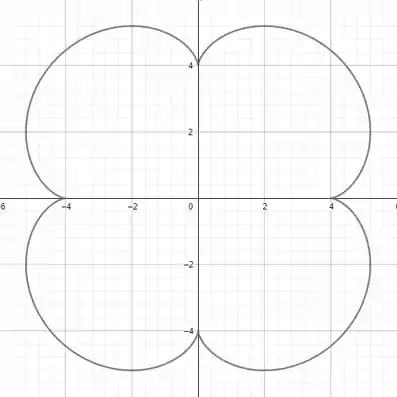
Então essa é nossa epicicloide. Está aí o gráfico que a questão pediu!
Passo 3
Para calcular a área, podemos usar:
Como enunciado traz, o traçado da epicicloide é baseado em uma circunferência rolando ao longo do interior de outra, portando podemos usar como limites do nosso parâmetro os limites de uma circunferência completa:
Esses são os limites de integração da nossa integral. Substituindo:
E os limites da integral, ficamos com:
Derivando para termos :
Fazendo a multiplicação dos termos:
Substituindo:
E rearranjando os termos:
Passo 4
A única integral que vai dar problema agora é no termo central, então calculando por partes temos
Usando
É só substituirmos:
Aplicando a integração por partes na segunda integral:
Substituindo:
Voltando para nossa soma:
Jogando a última integral da soma pro lado esquerdo da equação com o sinal trocado:
Dividindo toda a equação por :
Passo 5
Então nós pré calculamos a integral do termo do meio, e agora é só integrar o primeiro e o terceiro termo da soma abaixo, substituindo o valor da integral que encontramos no passo acima:
Todos os termos que tem quando ou , então nos sobra