Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.7 - Ex. 17
Considere a equação de onda
em um meio unidimensional infinito, sujeita às condições iniciais
- Usando a forma da solução obtida no Problema 13, mostre que
- Use a primeira das equações no item (a) para mostrar que . Depois use a segunda equação para mostrar que e, portanto, que
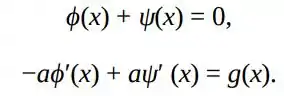
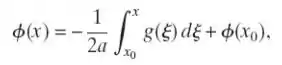
em que é arbitrário. Finalmente, determine .
(c) Mostre que
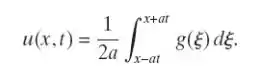
Passo 1
O resultado da questão nos informa que:
Aplicando a condição de contorno nós teremos que:
E aplicando a segunda condição de contorno () nós temos que:
Onde será:
Então nos dará:
Logo:
Que é o que queremos demonstrar para a letra a
Passo 2
Para a letra b nós temos que a primeira equação vale:
Ou seja:
Derivando em nós teremos:
E pela segunda equação nós tiramos que:
O que pode ser escrito como:
Onde , logo , logo:
Então o valor de para um intervalo arbitrário de será:
Onde é só uma variável qualquer para que você não faça nenhuma besteira na hora de integral e é somente um termo constante que só na hora que derivamos em relação a , por isso que é aplicado em pois não terá termos em .
O valor de terá o sinal inverso de e valerá:
Passo 3
Como:
Então:
Pois os termos de integração seguem o ponto aplicadas nas funções e , logo podemos escrever essa integral como: