Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.7 - Ex. 67

Considere a reta tangente a elipse x 2 a 2 + y 2 b 2 = 1 no ponto ( p , q ) no primeiro quadrante.

  1. Mostre que a linha tangente intercepta x em a 2 / p e y em b 2 / q
  2. Mostre que a porção da reta tangente que corta os eixos tem comprimento mínimo a + b ;
  3. Mostre que o triângulo formado pela reta tangente e pelos eixos coordenados tem área mínima a b .

Passo 1

Eaee, belezinha??? Bom pessoal, a questão nos pede para considerar a seguinte elipse x 2 a 2 + y 2 b 2 = 1 com ponto p , q no primeiro quadrante:

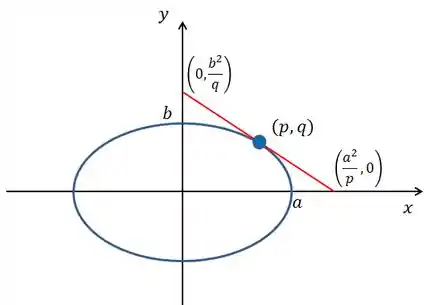
A questão nos pede para fazermos várias demonstrações com essas informações.

Então vamos fazendo uma por uma para ficar melhor da gente entender, combinado??

Bora lá!! 😉

Passo 2

Primeiramente queremos mostrar que a linha tangente intercepta x em a 2 p e y em b 2 q .

Bom... sabemos que a equação da reta é dada por:

y = m x + n

O coeficiente angular m pode ser encontrado pela primeira derivada da função:

y ' = m

No ponto ( p , q ) , temos:

q = y ' p + n

n = q - p y '

Agora vamos para a elipse:

x 2 a 2 + y 2 b 2 = 1

A derivada implícita é dada por:

2 x a 2 + 2 y y ' b 2 = 0

Isolando o y ’ :

y ' = - b 2 x a 2 y

No ponto ( p , q ) , temos:

y ' = - b 2 p a 2 q

Passo 3

Como vimos acima, y ’ é o coeficiente angular da reta y ' = m . Então jogando este valor na equação:

y = - b 2 p a 2 q x + n

Onde: n = q - p y ' = q + b 2 p 2 a 2 q

Então:

y = - b 2 p a 2 q x + q + b 2 p a 2 q ∴

y = - b 2 p a 2 q x + a 2 q 2 + b 2 p 2 a 2 q

Temos ainda, que a elipse no ponto ( p , q ) é dada por:

p 2 a 2 + q 2 b 2 = 1 → p 2 = a 2 - a 2 q 2 b 2

Substituindo p 2 na equação da reta:

y = - b 2 p a 2 q x + a 2 q 2 + b 2 a 2 - a 2 q 2 b 2 a 2 q ∴

y = - b 2 p a 2 q x + q 2 + b 2 1 - q 2 b 2 q ∴

y = - b 2 p a 2 q x + q 2 + b 2 - q 2 q

Finalmente, temos uma equação simplificada da reta:

y = - b 2 p a 2 q x + b 2 q

Passo 4

a) Agora, vamos encontrar os pontos de interseção com os eixos.

x = 0 → y = b 2 q

y = 0 → 0 = - b 2 p a 2 q x + b 2 q

x = a 2 p

b) Agora, para encontrar o comprimento da reta L entre os pontos de interseção (reta em vermelho na figura), podemos usar pitagoras:

L = a 2 p 2 + b 2 q 2 = a 4 p 2 + b 4 q 2

Temos que eliminar o p e q da equação para se adequar ao que foi pedido no enunciado.

Para isto, vamos usar a relação da elipse:

p 2 a 2 + q 2 b 2 = 1 → p 2 = a 2 - a 2 q 2 b 2

Substituindo:

a 4 p 2 + b 4 q 2 = a 4 a 2 - a 2 q 2 b 2 + b 4 q 2 = a 2 b 2 b 2 - q 2 + b 4 q 2

Passo 5

Vamos agora chamar o quadrado desta função de q F q :

F q = a 2 b 2 b 2 - q 2 + b 4 q 2

Observe que para q → 0   e   p a r a   q → b , temos que F q → ∞ . Portanto, entre 0 e q deve existir um valor de mínimo.

Iremos encontrar este mínimo achando o valor crítico de q :

F ' q = 0 ∴

F ' q = 2 a 2 b 2 q b 2 - q 2 2 - 2 b 4 q 3 = 0 ∴

a 2 q b 2 - q 2 2 = b 2 q 3 ∴

a 2 q 4 = b 2 b 2 - q 2 2

Tirando a raiz de tudo:

a q 2 = b ( b 2 - q 2 )   ∴

a + b q 2 = b 3 ∴

q 2 = b 3 a + b

Agora vamos substituir este valor na equação de F ( q ) :

F q = a 2 b 2 b 2 - b 3 a + b + b 4 b 3 a + b ∴

= a + b a 2 b 2 ( a + b ) b 2 - b 3 + a + b b 1 ∴

= a + b a 2 ( a + b ) - b + a + b b 1 ∴

= a + b a + a + b b ∴

a + b 2

Portanto, é verdade que:

a + b 2 > a + b

Passo 6

Show de bola, agora queremos encontrar a área mínima desse triangulo formado por essa reta e pelos eixos coordenados. A área de um triangulo é dada por:

A = 1 2 b × h ⇒ A = a 2 b 2 2 p q  

Mas temos que além disso, a equação da elipse fornece pra gente as seguintes coordenadas

x 2 a 2 + y 2 b 2 = 1 ⇒ p 2 a 2 + q 2 b 2 = 1

b 2 p 2 + a 2 q 2 = a 2 b 2

Isolando p nessa equação, temos que

b 2 p 2 = a 2 b 2 - a ² q ²

p 2 = a 2 - a 2 b 2 q ²

p 2 = a 2 1 - q 2 b 2

p = a 1 - q 2 b 2

Substituindo na equação da área, temos que

A = a 2 b 2 2 p q = a 2 b 2 2 a 1 - q 2 b 2 q

A = a b 2 2 q 1 - q 2 b 2 = a b 3 2 q b 2 - q ²

Passo 7

Como queremos a área mínima, devemos derivar essa função e encontrar seus pontos críticos igualando a zero, dessa forma temos que

d A d q = - a b 3 - 2 q 2 + b 2 2 q 2 b 2 - q 2 b 2 - q 2 = 0

a b 3 - 2 q 2 + b 2 = 0

2 q 2 = b ²

q = b 2 = 2 b 2

Logo, o valor de q que minimiza a área é dado por q = 2 b 2 , e como temos a relação com p , então

p = a 1 - q 2 b 2

p = a 1 - 2 b 2 2 b 2 = a 1 - 2 4 = 2 a 2

Logo a área mínima será:

A = a 2 b 2 2 p q

A = a 2 b 2 2 2 a 2 2 b 2 = a 2 b 2 a b

A = a b

Entendeu direitinho?? Responde aee 😉

Resposta

Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o nível de produção no qual a função custo marginal começa a crescer. C x = 0,0002 x 3 - 0,25 x 2 + 4 x + 1500
Para a função custo e demanda dada, encontre o nível de produção que maximizará o lucro. C x = 1450 + 36 x - x 2 + 0,001 x 3 ,p x = 60 - 0,01 x
Uma função custo é dada.Encontre as funções custo médio e custo marginal.Use os gráficos das funções na parte (a) para estimar o nível de produção que minimize o custo médio.Use o cálculo para encontr
Encontre o nível de produção no qual a função custo marginal começa a crescer. C x = 0,001 x 3 - 0,3 x 2 + 6 x + 900
Um fabricante de aviões quer determinar o melhor preço de venda para um novo produto. A companhia estima que o custo inicial de planejamento do avião e montagem das fábricas nas quais ele será produzi