Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 78
Demonstre, usando a definição 9, que
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui iremos eu e você utilizarmos da definição 9 para provar o limite que nos foi dado.
A definição 9 diz que:
Seja uma função com o domínio . Então:
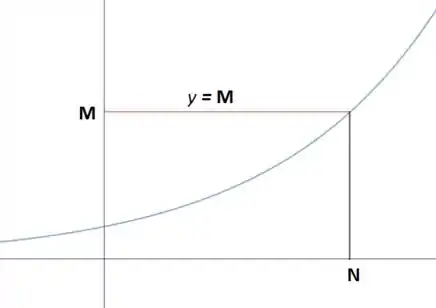
Se existir qualquer numero positivo M, então existe um numero N tal que:
Se então
Passo 2
Para provar que
Nós precisamos provar que para todo , existe um tal que:
Se então
é um numero positivo, então podemos escrever . Onde é outro numero positivo.
Subtraindo em ambos os lados:
Nós iremos utilizar
Porém
é um numero positivo, por conta de que e são positivos.
Nos é permitido dividir ambos os lados da inequação por um numero positivo. Dividindo ambos por , encontramos:
Para cada , existe , tal que
Então provamos o que nos foi pedido.
Resposta
Ver o desenvolvimento.