Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1j
Desenhe a curva dada (coordenadas polares ).
Passo 1
Para esse caso, analisamos que:
Ou seja, o vai variar entre 2 e 0. O que significa que o raio nunca é negativo e por ser uma função somada a vai ter uma simetria com o eixo de .
Passo 2
A tabela vai ficar assim:
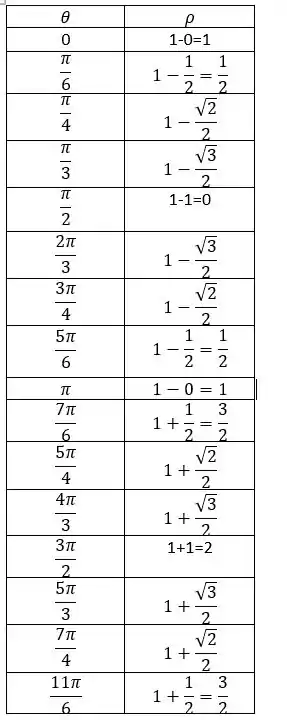
Passo 3
Depois de localizarmos os raios, vamos chegar em:
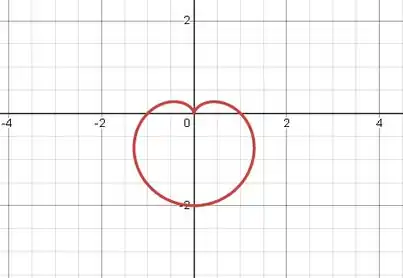
Resposta
Exercícios de Livros Relacionados
Determine a área das regiões compreendidas entre y = 8 c o s ( x ) e y = s e c( x ) 2 ,- π 3 ≤ x ≤ π 3
Determine a área entre a curva y = l n x , y = l n 2 x de x = 1 até x = 5 .
Determine a área das região em forma de hélice compreendida entre a curva x - y 1 3 = 0 e x - y 1 5 = 0
Determine a área das regiões compreendidas entre x = t g 2 ( y ) e x = - t g 2 ( y ) ,- π 4 ≤ y ≤ π 4
Determine a área das regiões compreendidas entre y = sec 2 x e y = t g 2 ( x ) , ,- π 4 ≤ x ≤ π 4