Determine a área das regiões compreendidas entre

e ,

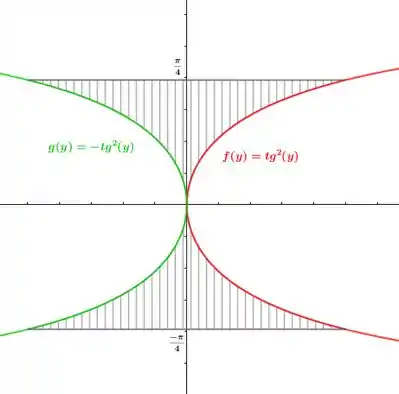Esboçando o gráfico da função, seja por um software, ou substituindo alguns valores em cada umas das funções para obter pontos, teremos um gráfico como esse ou parecido,

Onde, pelo que podemos ver é a função que está à frente , é a função que está atrás e a parte hachurada é região que desejamos calcular a área.

Sendo assim, pela definição temos que a integral da região será:

Utilizamos este intervalo de integração, pois foi dado no enunciado da questão.

Já que já encontramos a “cara” integral que para determinar a área, então vamos partir para os cálculos e ver quando essa integral vai dar. Sendo assim,

Usando a propriedade de tirar a constante de dentro da integral,

Usando o fato de +1== Daí,

Usando a regra da subtração (integral da subtração é a subtração das integrais)

Usando o Teorema Fundamental do Cálculo Parte II,

Usando o fato de

Como ,

Logo,