- Desenhe ilustrações como as das Figuras 10.7 e 10.8 para mostrar que as somas parciais da série harmônica satisfaz as desigualdades
- Não existe absolutamente nenhuma evidência empírica para a divergência da série harmônica, mesmo que saibamos que ela diverge. As somas parciais simplesmente aumentam muito lentamente. Para compreender o que estamos dizendo, suponha que você tenha começado com no dia em que o universo foi criado, 13 bilhões de anos atrás, e adicionado um novo termo a cada segundo. Quão grande aproximadamente a soma parcial seria hoje, considerando um ano com 365 dias?
Passo 1
Oi pessoal, vem comigo!
Primeiramente iremos fazer a curva de a , temos:
Gerando a seguinte curva:
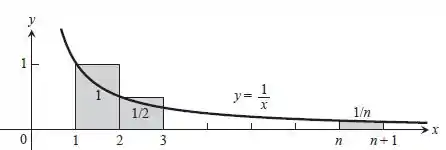
Para a curva de a , temos:
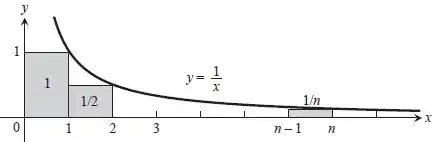
Passo 2
Como a série é positiva, contínua e decrescente para , podemos utilizar o teste da integral, para encontrarmos o valor da soma
Como no enunciado fala que adiciona um novo termo a cada segundo, sendo que 1 ano tem 365 dias:
Como queremos para 13 bilhões de anos:
Então temos:
Resposta
- Resposta no Passo 1.
- .