1. Desenhe a imagem:
m)
Passo 1
O par de coordenadas (x,y,z) da nossa questão é , faremos
, e
Faremos uma tabela de alguns valores e então ligaremos os pontos e criaremos nossa imagem.
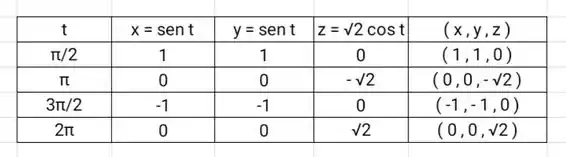
Resposta
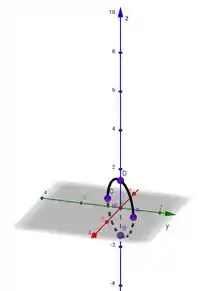
1. Desenhe a imagem:
m)
O par de coordenadas (x,y,z) da nossa questão é , faremos
, e
Faremos uma tabela de alguns valores e então ligaremos os pontos e criaremos nossa imagem.

