9. Determine a função , cujo gráfico passa pelo ponto e que goza da propriedade : a área do triangulo de vértices , e , é igual a , para todo no gráfico de , onde é a interseção da reta tangente em com o eixo .
Passo 1
Fazendo uma ilustração do triângulo, temos o seguinte:
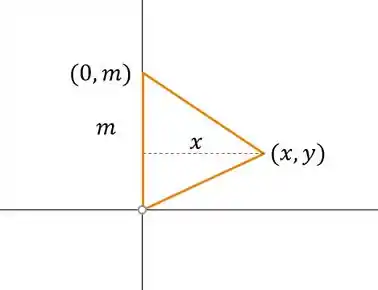
Para achar a área, vamos o seguinte:
Assim,
Como a área é sempre 1:
Passo 2
Agora vamos dar uma olhada para a reta tangente ao gráfico de . Como o coeficiente angular é a derivada no ponto e o ponto:
Mas o ponto pertence a reta. Assim,
Substituindo em :
Arrumando as coisas:
Passo 3
Para resolvermos uma EDO 1º ordem não homogênea, fazemos o seguinte:
- Deixamos a EDO no seguinte formato :
- Agora vamos calcular o fator integrante:
- Por último, multiplicamos a EDO por e finalizamos!
Então, dividindo nossa expressão por :
Assim,
Portanto,
Multiplicando por :
Isto é,
A ideia de fazer isso é que o nosso lado esquerdo sempre fica o seguinte:
Passo 4
Por fim, temos o seguinte:
Não esquece:quando
Integrando:
Portanto,
Usando que o ponto pertence a curva:
Reescrevendo nossa curva: