Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 51d
Determine o volume do sólido obtido com a rotação da região limitada por e pelas retas e em torno
- Do eixo .
- Do eixo .
- Da reta .
- Da reta .
Passo 1
Precisamos obter o volume de um sólido de revolução obtido através da rotação de uma região em relação aos eixos coordenados, e , e em relação a retas paralelas a eles. Para cada um dos casos, discutiremos um pouco a metodologia necessária para calculá-los. Entretanto, todos eles possuem uma necessidade em comum: esboçar a região limitada! Começaremos por entender como é esta região.
Passo 2
Vamos começar por esboçar a nossa região limitada pelas curvas.
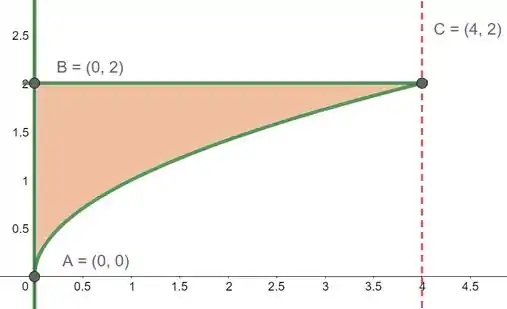
Em destaque temos a região limitada pelas curvas e em vermelho o nosso eixo de rotação. Como queremos obter a rotação em torno da reta , uma reta paralela ao eixo , utilizaremos o método dos anéis. Este método nos diz que o volume do sólido é dado pela seguinte integral:
Em que e são as funções que definem os raios externos e internos da nossa figura. Vamos repetir a nossa figura da região para deixar claro quem são essas curvas!
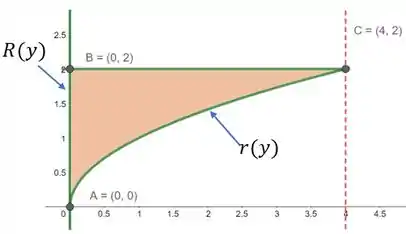
Agora fica claro quem são nossas funções! Em relação ao nosso sistema de coordenadas inicial, elas são:
Passo 3
Podemos partir logo para a integração agora que determinamos as curvas? A resposta é simples e clara: não!! Calma, não sejamos apressados!
As funções e que obtivemos estão escritas em relação ao nosso sistema de coordenadas original: origem, eixo e eixo . Precisamos escrever estas curvas em relação ao nosso eixo de rotação. Para isto, é necessário fazer uma translação vertical. Como o eixo corresponde à reta transladada para à esquerda em 4 unidades, as nossas funções devem ser transladadas para à esquerda em 4 unidades também! Portanto, temos:
Passo 4
Agora sim! Obtivemos as curvas em relação a nossa reta de rotação e só nos falta determinar os limites de integração. Para isto, basta responder a seguinte pergunta: qual o menor e o maior valor de na nossa região? Eles são 0 e 2, respectivamente. Agora sim, vamos calcular a nossa integral!