2) Calcule o volume dos sólidos abaixo:
g)
Passo 1
Vamos lá. Antes de começar a fazer umas continhas, vamos entender que sólido é esse. Temos a equação de uma esfera e a de um cilindro, teremos algo parecido com:
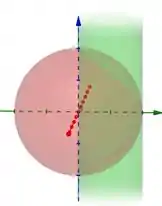
O sólido que queremos calcular o volume está compreendido na interseção entre a esfera e o cilindro. A esfera (vermelho) está sendo cortada por esse cilindro (verde). A esfera tem raio , enquanto o cilindro tem o raio . A gente pode ver isso, analisando a expressão que foi fornecida. Para o cilindro, temos:
Completando quadrados, teremos:
Para a esfera temos:
Podemos ver que o raio dessa esfera será
Passo 2
Okay, agora já sabemos algumas coisas a respeito desse sólido aí. Agora, para calcular o volume desse sólido, precisamos calcular a seguinte integral:
Mas não é tão interessante calcular essa integral dessa maneira, então vamos mudar essas variáveis, vamos mudar as variáveis para um sistema de coordenadas cilíndricas, utilizando:
Temos que o jacobiano da mudança de coordenadas cilíndricas é dado por . Assim, vamos calcular a seguinte integral:
Passo 3
Vamos agora encontrar os intervalos de integração que vamos utilizar.
Começando por , teremos que:
Ou seja, teremos que irá variar de
Em , teremos o seguinte:
Ou seja, teremos uma variação em de .
Em , teremos uma variação de . Isso é por causa que o cilindro não ocupa todo o plano cartesiano, apenas metade dele, não rotacionando por todo o plano. Podemos observar isso olhando de uma outra perspectiva, note:
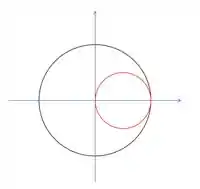
Em vermelho temos o cilindro, dentro da esfera.
Passo 4
Agora vamos calcular a integral, temos então:
Agora repare o seguinte: Para a integração em , podemos simplificar nossa integral justamente por ela ser simétrica. Podemos fazer a integral considerando o intervalo . Dessa forma, podemos multiplicar por 2 a integral e encontraremos o mesmo valor!
Ficamos então com:
Resolvendo a primeira integral:
Essa integral em parece ser um pouco complicada, mas não é tanto assim. Para resolver essa integral, vamos fazer uma substituição:
Dessa forma, teremos:
Ou seja:
Aplicando nos limites de integração, teremos o seguinte:
Repare que podemos simplificar essa última expressão, se lembrarmos que
Com essa arma poderosíssima, temos o seguinte:
Dessa forma:
Aplicando naquela integral que queríamos resolver, teremos:
Simplificando mais um pouco, teremos o seguinte:
Resolvendo a integral, temos:
Simplificando, temos:
Agora jogamos esse resultando na integral que estávamos resolvendo:
Substituindo o valor da integral de dentro, temos:
Agora repare! Antes da gente sair fazendo substituição outra vez! A função é uma função ímpar! A gente pode verificar isso justamente por que:
Além disso, ela é simétrica em torno de . Sendo assim, a integral dessa função de até , por definição, será nula! Isso poupa muito trabalho pra gente, viu? 😊
Agora, nossa integral será:
Resposta
Daí, o volume do sólido é .