Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 3

Calcule int_0^2 d x int_0^(sqrt(2 x - x^2)) d y int_0^a z sqrt(x^2 + y^2) d z .

Passo 1

Vamos encarar juntos essa questão aí, vão bora!

Se formos calcular essa integral da maneira como ela está, sentiremos uma certa dificuldade. Vamos pegar o limite de integração relacionado a y, e vamos ver em que espaço estamos integrando.

Temos,

sqrt(2 x - x^2) = y

2 x - x^2 = y^2

x^2 + y^2 = 2 x -> (x - 1)^2 + y^2 = 1

Beleza, temos uma circunferência deslocada no plano XY de raio 1. Como estamos trabalhando em 3 dimensões e temos uma componente z, vamos aplicar uma mudança de variáveis utilizando coordenadas cilíndricas, daí:

{[[x = r cos theta],[y = r sen theta],[z = z]])

Lembrando que o jacobiano das coordenadas cilíndricas é dado por |J| = r .

Passo 2

Beleza, estamos no caminho. A nossa integral em coordenadas cilíndricas vai ter essa cara:

int_0^a int int z sqrt(x^2 + y^2) r d r d theta d z -> int_0^a int int z sqrt(r^2 ( sen^2 theta + cos^2 theta )) r d r d theta d z = int_0^a int int z sqrt(r^2) r d r d theta d z = int_0^a int int z r^2 d r d theta d z

Vamos então descobrir os intervalos de integração que usaremos.

Temos que para r , teremos que:

x^2 + y^2 = 2 x

r^2 (sen^2 theta + cos^2 theta) = 2 r cos theta -> r = 2 cos theta

Assim, 0 <= r <= 2 cos theta .

Para theta , observe a figura.

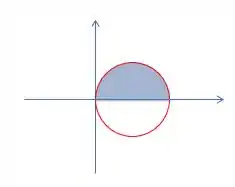
Essa é a circunferência dada por (x - 1)^2 + y^2 = 1 . Observe que, no nosso intervalo, estamos tratando com um valor positivo, ou seja, só a parte superior da circunferência. Daí, teremos que para formar esse pedaço da circunferência, a variação de theta deve ser de 0 <= theta <= pi // 2 .

Passo 3

Daí, calculando a integral:

int_0^a int_0^((pi)/(2)) int_0^(2 cos theta) r^2 z d r d theta d z = int_0^a int_0^((pi)/(2)) (8)/(3) cos^3 theta z d theta d z = (8)/(3) int_0^a z [1 - (1)/(3)] d z = (16)/(9) int_0^a z d z = (8)/(9) a^2

Resposta

O resultado da integral é (8)/(9) a^2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a massa do cilindro x 2 + y 2 ≤ 4 e 0 ≤ z ≤ 2 , sabendo que a densidade no ponto x , y , z é o dobro da distância do ponto ao plano z = 0 .
8. Seja B ⊂ ℝ3 e sejam f e g duas funções contínuas em B. Suponha que,para toda bola B1 ⊂ B, ∫ ∫ ∫ B 1 f x , y , z d x d y d z =∫ ∫ ∫ B 1 g x , y , z d x d y d z Prove que f (x, y, z) = g (x, y, z) em
11. Calcule ∫ ∫ ∫ B 1 x 2 d x d y d z onde B é o conjunto de todos (x, y, z) tais que 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 e z = 2. Compare com o Exercício 10 e explique.
9. Seja B ⊂ ℝ3 uma bola fechada e seja f: B → ℝ uma função contínua,com f (x, y, z) 0 em B. Prove que ∫ ∫ ∫ B 1 f x , y , z d x d y d z0
10. Seja B ⊂ ℝ3 um conjunto limitado, com fronteira de conteúdo nulo, eseja f: B → ℝ uma função contínua tal que f (x, y, z) ≥ 0 em B. Suponhaque ∫ ∫ ∫ B 1 f x , y , z d x d y d z = 0 Prove que f (x,