Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 35

Encontre a área sobre um arco de trocoide do Exercício 40, na seção 10.1, para o caso de

Passo 1

Do problema mencionado no enunciado temos definidas as equações paramétricas do trocoide como:

Mas tá, e de onde vem isso?

Podemos pegar o intervalo de até com para entendermos de onde vêm essa fórmula, teremos a seguinte figura rosa (nesse caso específico foi usado como exemplo):

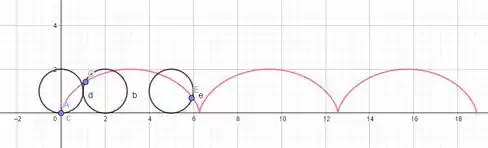
Esse problema onde é de uma curva específica chamada cicloide. Bora entender o que ela significa?

Pensa em uma roda de bicicleta se movendo (ela é o círculo preto), agora vamos pegar um ponto qualquer desde que esteja no raio dela. Conforme andamos com essa roda, esse ponto vai desenhando essa curva que vemos na figura. Vamos dar um zoom na segunda circunferência:

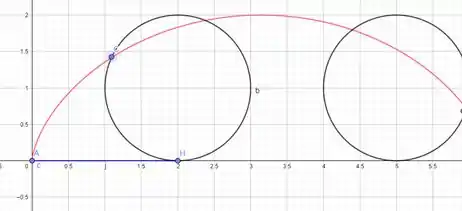
Passo 2

Perceba que a distância do segmento de reta azul é exatamente o quanto a circunferência andou (distância de até a intersecção com a curva rosa)! Então, se estamos falando de arco, a distância vai ser o raio da circunferência multiplicado pelo ângulo que ele andou, ou seja, Beleza, metade da formula já temos, mas as coordenadas de e não podem ser para e para , alguma coisa tem que ser retirada e acrescentada para que o ponto esteja sempre nessa “intersecção”. Essa coisa é a projeção do ponto sobre os eixos denominada e para respectivamente.

Para chegar na fórmula é só pensar num ponto dentro da roda, ao invés de estar nela, e aí a distância que vamos retirar ou acrescentar será e não .

Passo 3

Bom, agora que já entendemos o significado dessas curvas, e sabemos que para cada arco a circunferência dá uma volta completa, ou seja podemos encontrar a área dentro de um arco qualquer usando os limites de integração de até .