Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 3
Encontre a área da região sombreada.
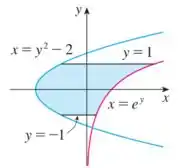
Passo 1
Bora lá!! A gente quer achar a área da região sombreada, que no nosso desenho aqui �� a região rosinha!
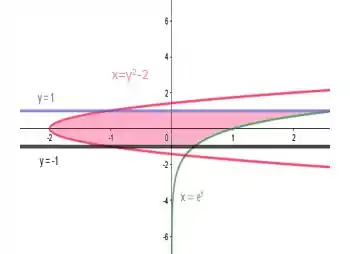
E como a gente acha essa área?!
A gente tem essa fórmula geral aqui:
Mas e agora?! Quem é e ? Quem vão ser os limites de integração?
Bem, e vão ser as curvas! O é “right”, direita em inglês e o é “left” esquerda em inglês Ou seja, curva da direita e curva da esquerda!
Passo 2
Analisando a nossa figura, vemos que:
Agora os limites de integração! Se a gente reparar, essas duas curvas são delimitadas por duas retas:
Então esses vão ser nossos limites de integração.
Agora vamos substituir na integral!! 😉
Passo 3
Já sabemos o que temos que fazer, então agora vamos substituir e na integral:
Substituindo:
Podemos separar cada elemento dessa integral:
Resolvendo:
Aplicando os limites de integração:
Calculando tudinho, temos:
Prontinho!