Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.5 - Ex. 41
Encontre as assíntotas horizontal e vertical e trace um esboço do gráfico da função
Passo 1
Vamos começar pelas assíntotas horizontais.
Para encontra-las demos que calcular dois limites
E
Se algum desses limites der algum número, então teremos assíntotas horizontais.
Vamos começar com
Temos que vai para quando
Isso porque
Aquele não vai influenciar no . Então o denominador vai para
Quando temos um número sobre esse limite vai para
Assim, temos
Como uma assíntota horizontal.
Passo 2
Temos que vai para quando
Isso porque
Aquele não vai influenciar no . Então o denominador vai para
Quando temos um número sobre esse limite vai para
Assim, temos
Como uma assíntota horizontal.
Passo 3
A assíntota vertical é o valor de que ao tomarmos o limite ele vai para ou para .
Para acharmos essas assíntotas, precisamos calcular o limite em alguns candidatos.
Quem são eles?
Como aqui temos uma fração, os candidatos serão os que zeram o denominador.
Nesse caso
Para o cálculo da assíntota, devemos separar nos limites laterais para cada valor de . Só que aqui, temos que tomar cuidado com um detalhe importante.
Temos o dentro de uma raiz quadrada. Então ele não pode ser negativo, dessa forma, se pegarmos valores entre e , ao elevarmos ao quadrado vai dar menor que , então não podemos pegar nada nesse intervalo.
Mas o que isso significa para nós? Não vamos nos preocupar com os limites laterais pela direita de e pela esquerda de , para não pegarmos números nesse intervalo,
Assim, vamos olhar apenas os seguintes limites laterais.
E
Passo 4
Começando com
Que vai ser
Opa, deu um número sobre . Então esse limite vai para ou para . Basta olharmos o sinal de próximo de , neste caso, pela direita.
Aqui não precisamos ficar achando lógicas loucas, basta olhar que raiz quadrada é sempre positiva, então aquela fração sempre vai ser positiva.
E isso nos diz que
Como achamos pelo menos um dos limites laterais indo para , temos que
É assíntota vertical.
Passo 5
Começando com
Que vai ser
Opa, deu um número sobre . Então esse limite vai para ou para . Basta olharmos o sinal de próximo de , neste caso, pela esquerda.
Aqui não precisamos ficar achando lógicas loucas, basta olhar que raiz quadrada é sempre positiva, então aquela fração sempre vai ser positiva.
E isso nos diz que
Como achamos pelo menos um dos limites laterais indo para , temos que
É assíntota vertical.
Passo 6
No final temos
E
Como assíntotas verticais.
Vamos juntar com nossa assíntota horizontal
E ver como fica o esboço.
O esboço vai ficar
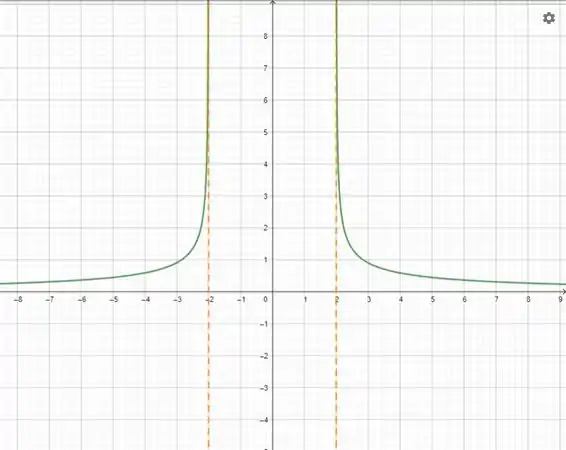
Resposta
Assíntota horizontal:
Assíntota vertical:
