Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 23

Encontre a primitiva F de f que satisfaça a condição dada. Verifique sua resposta comparando os gráficos de f e F

f x = 5 x 4 - 2 x 5 ,     F 0 = 4

Passo 1

E aí! como vai?

Bom pessoal, nessa questão temos uma função:

f x = 5 x 4 - 2 x 5

E queremos encontrar a primitiva F x dessa função.

Para achar F vamos ter que achar a antiderivada geral, sabemos que uma função F é chamada de antiderivada (ou primitiva) de f :

F ' x = f x

E se F é uma antiderivada de f nesse intervalo, então a antiderivada mais geral de f :

F x + C

onde C é uma constante qualquer, afinal, quando derivamos a constante obtemos zero, logo somar uma constante a F x não muda em nada sua derivada.

Aqui vai nos ajudar saber a regra de antiderivada do polinômio e da constante:

K = K x '

x n = x n + 1 n + 1 '

Depois de encontrarmos F , vamos usar a condição dada que é:

F 0 = 4

Para encontrar o valor da constante C .

Por fim vamos colcoar o gráfico de f e de F lado a lado para verificar se de fato f é a derivada de F .

Passo 2

Para encontrar a primitiva de f ( x ) , iremos utilizar a regra do polinômio, assim, temos

f x = 5 x 4 - 2 x 5

Para o primeiro termo:

5 x 4 = 5 x 5 5 '

5 x 4 = x 5 '

E para o segundo termo temos:

- 2 x 5 = - 2 x 6 6 '

- 2 x 5 = - x 6 3 '

Agora somando tudo com uma constante temos:

F x = x 5 - 1 3 x 6 + C

Derivando F ( x ) , temos

F ' x = 5 x 4 - 2 x 5

Como F ' x = f ( x ) , então F ( x ) é a primitiva de f ( x ) .

Show?

Passo 3

Substituindo a condição dada, temos

F x = x 5 - 1 3 x 6 + C

F 0 = 0 5 - 1 3 0 6 + C

C = 4

Então, temos que

F x = x 5 - 1 3 x 6 + 4

Passo 4

Podemos assim gerar o gráfico de f ( x ) e F ( x )

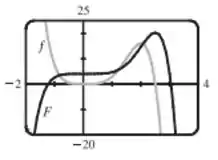
Podemos ver que f é positiva quando F está crescendo e negativa quando F está decrescendo. Podemos ver também que em f x = 0 , F ( x ) possui um máximo local.

E aí! entendeu tudo? Responde Aí!

Resposta

F x = x 5 - 1 3 x 6 + 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema de valor inicial (d^2 y)/(d x^2) = sec^2 x y (0) = 0 y^' (0) = 1
Resolva o problema de valor inicial (d^2 y)/(d t^2) = 1 - e^(2 t) y (1) = - 1 y^' (1) = 0
Nos Exercícios 35-38, resolva o problema de valor inicial.38- y - 2 d x d y = e x e 2 x + 1 ,y 0 = 1
Nos Exercícios 31-34, resolva a equação diferencial.33- y y ' = sec ⁡ y 2 sec 2 ⁡ x
Nos Exercícios 35-38, resolva o problema de valor inicial.35- d y d x = e - x - y - 2 ,y 0 = - 2