Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 61
Encontre o valor médio de na região .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Ela pede pra gente encontrar o valor médio de uma função em uma região . Pra achar isso, a gente só precisa resolver essa expressão:
Onde é a área da região de integração.
Pra resolver isso, a gente vai primeiro analisar quem é , pra calcular o , e depois a integral . Por fim, colocamos tudo na fórmula do !
Passo 2
A questão fala que é um triângulo e nos dá os vértices. Vamos desenhar ele então:
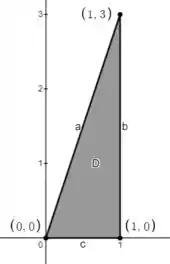
A gente consegue definir o como limitado por essas três retas que eu chamei de , e , que são os lados do triângulo.
Então vamos encontrar que retas são essas.
A reta passa por e . O coeficiente angular é:
O coeficiente linear é , porque a reta corta o eixo na origem, então:
A reta é uma reta horizontal:
A reta é o próprio eixo :
Com isso, a gente pode definir a região como a região onde o está entre e , e o varia de até :
Para calcular a área dessa região, é só usarmos a fórmula da área do triângulo:
Passo 3
Como os limites de integração são:
Nossa integral iterada fica:
Passo 4
Calculando primeiro em função de , consideramos constante, então ele pode sair da integral:
Integrando em :
Ficamos então com uma integral simples em função de :
Por último, integrando em :
Encontramos o valor da integral:
Passo 5
Falta só substituir tudo na fórmula: