Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 48
Determine o valor médio de sobre o retângulo dado:
Passo 1
E ai, galerinha, beleza??
A gente vai ter que calcular o valor médio de uma função sobre um retângulo.
O valor médio de uma função é um valor que quando multiplicado pela área da região dá o volume do sólido de sobre , e é calculado assim:
Então a gente primeiro vai calcular a área de , depois a integral de sobre e assim achamos o valor médio!
Passo 2
Vamos lá, primeiro vamos ver como é esse retângulo.
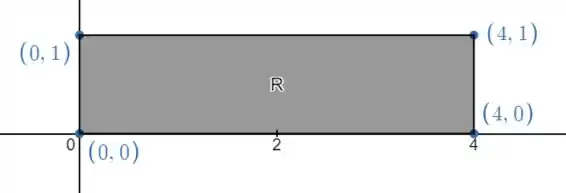
Assim, a gente já tem os intervalos de integração, e a área é calculada como:
Passo 3
O valor médio então é encontrado assim:
Começamos integrando em , com constante:
Pra calcular essa integral, vamos usar uma substituição:
Agora retornando pra variável original:
Passo 4
Vamos integrar em agora.
Vamos calcular essas duas integrais separadas, em ambas vamos usar substituição:
A segunda integral fica:
Juntando tudo:
E esse é o valor médio!