Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 38

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .

Passo 1

Vamos calcular o volume com a rotação em relação x = 1 . Vamos aqui usar o método das cascas.

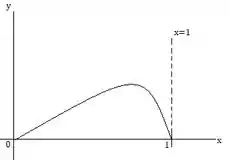
O volume é dado por:

V = ∫ a b 2 π x f x d x

Substituindo na integral, temos:

V = ∫ 0 1 2 π 1 - x x 1 - x 2 d x

V = 2 π ∫ 0 1 x 1 - x 2 d x - 2 π ∫ 0 1 x 2 1 - x 2 d x = 2 π V 1 - 2 π V 2

Passo 2

Como dividimos a integral em duas, vamos resolver uma de cada vez. Primeiramente, vamos olhar para V 1 .

V 1 = ∫ 0 1 x 1 - x 2 d x

Para resolver essa integral vamos usar o método da substituição de variáveis. Seja u = 1 - x 2   → d u = - 2 x d x . Assim:

V 1 = ∫ u ( - 1 2 d u ) = - 1 2 ∫ u 1 2 d u

V 1 = - 1 2 u 3 2 3 2

Retornando para a variável original:

V 1 = - 1 2 1 - x 2 3 2 3 2 0 1

V 1 = - 1 2 - 1 3 2 3 2 = 1 3

Passo 3

Agora, resolvendo a integral V 2 :

V 2 = ∫ 0 1 x 2 1 - x 2

Seja x = s e n θ     →   d x = c o s θ d θ . Assim,

V 2 = ∫ 0 π 2 s e n 2 θ c o s θ   c o s θ   d θ = ∫ 0 π 2 s e n 2 θ cos 2 ⁡ θ d θ

V 2 = ∫ 0 π / 2 1 4 2 s e n θ c o s θ 2 d θ = 1 4 ∫ 0 π / 2   s e n 2 2 θ   d θ

V 2 = 1 4 ∫ 0 π 2 1 2 1 - c o s 2 θ d θ = 1 8 θ - 1 2 s e n 2 θ 0 π 2

V 2 = 1 8 π 2 = π 16

Passo 4

Agora que temos os valores de V 1 e V 2 , podemos encontrar o valor final de V !

V = 2 π 1 3 - 2 π π 16

V = 2 3 π - 1 8 π 2

Resposta

O valor de V é igual a:

V = 2 3 π - 1 8 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 63 a 94, calcule a integral definida. 6 7 . ∫ 0 2 t 3 d t 4 + t 2
Calcule a integral indefinida. ∫ 1 x 2a 2 + x 2d x
Calcule a integral indefinida. ∫ t2 t - t 2d t
Calcule a integral definida. ∫ 2 / 2 1 x 3 2 - x 2d x
Sejam m e n constantes não nulas dadas. Verifique que ∫ m u + n 1 + u 2 d u = m 2 ln ⁡ 1 + u 2 + n arctg ⁡ u + k