Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 4
Seja , em que é a função cujo gráfico é mostrado. (a) Calcule ; (b) Estime para ; (c) Em que intervalo está crescendo?; (d) Onde tem um valor máximo?; (e) Faça um esboço do gráfico de ; (f) Use o gráfico da parte (e) para esboçar o gráfico de . Compare com o gráfico de .
Passo 1
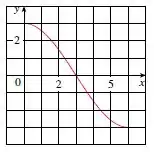
Opa, bora resolver essa questão?! Temos vários itens para responder, o enunciado nos dá o seguinte gráfico da função :
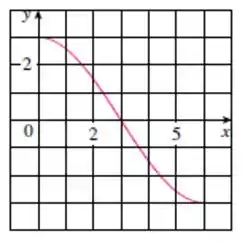
Sabendo que , a letra (a) pede pra a gente calcular .
Primeiro de tudo, vamos lembrar que a integral de uma função é a área embaixo da curva, no gráfico. E se essa área estiver abaixo do eixo x, então a integral tem valor negativo.
Então vamos la!
Como temos uma integral com os limites de integração iguais, o valor resultante dela é igual a zero. Para , teremos:
Isso porque que a área abaixo e acima do eixo são iguais, assim a “área positiva” cancela a “área negativa”. Sacou?!
Passo 2
Na letra (b) queremos estimar para . Vamos trazer o gráfico pra pertinho:
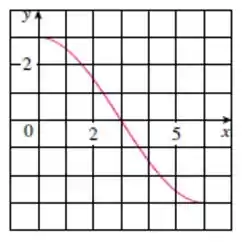
Para , o valor de compreende a área sob curva, de a , podemos aproximar essa área como um trapézio deitado, assim:
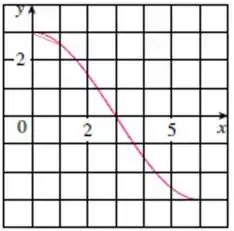
A base maior é igual a e a menor a gente pode estimar como . Já a altura vai ser igual a . Calculamos a integral como a área do trapézio:
Para fazemos a mesma coisa, assim:
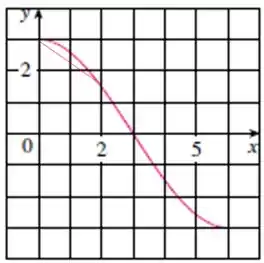
A base maior mede e a menor podemos estimar como , a altura aqui é igual a . Assim:
Para , o valor de compreende a área abaixo da curva, de a . Usando a mesma técnica de aproximação ficamos com um triângulo:
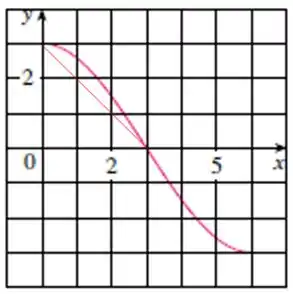
para temos uma parte da curva abaixo do eixo , assim vamos fazer:
Para o intervalo podemos aproximar como um triângulo:
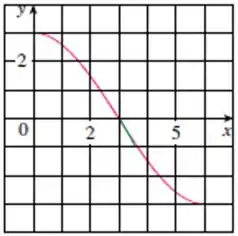
Vamos dizer estimar a base como:
Então:
Agora finalmente o último, . De novo podemos aproximar como um triângulo:
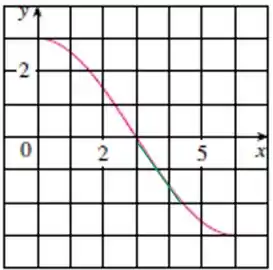
Podemos estimar a base como:
Assim:
Juntando com a parte positiva:
Passo 3
Na letra (c) queremos saber o intervalo em que está crescendo. Como podemos observar no passo anterior, a medida que andamos de para , o valor da função aumenta. Logo, é crescente no intervalo .
Passo 4
Na letra (d) queremos saber onde tem um ponto de máximo em . Bom, na letra (c) vimos que no intervalo a função é crescente e no intervalor [3,6] a função se torna descrescente. O ponto onde ocorre a troca de sentido é em . Logo, é onde possui valor máximo.
Passo 5
Aqui queremos esboçar o gráfico de . Bom, o gr��fico deve ter um ponto de máximo em , deve ser simétrico em relação a e ter raízes em e . Logo,
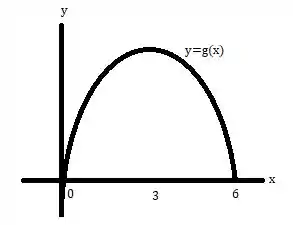
Passo 6
Lá do enunciado temos que:
Então o gráfico de deve ser igual ao gráfico de que é assim:
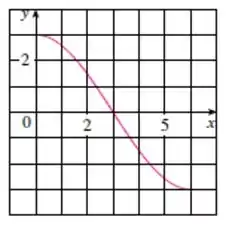
Prontinho!
Resposta
- ;
- aumenta no intervalo (0,3);
- tem valor máximo em ;