Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 28

Esboce a área da região que está dentro da primeira curva e fora da segunda curva.

r = 1 + cos ⁡ θ ,               r = 3 cos ⁡ θ

Passo 1

O problema pede para acharmos a área da região dentro da curva r = 1 + cos ⁡ θ e fora da curva r = 3 cos ⁡ θ .

Primeira coisa que temos que fazer é construir o gráfico, assim temos umas noção de qual área precisamos calcular. Sacou?

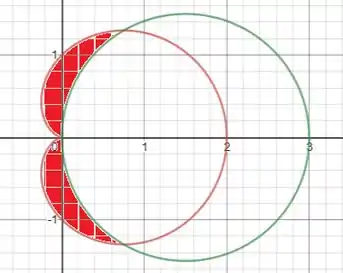
Para saber os limites de integração, temos que achar onde as curvas de cortam:

r = 1 + cos ⁡ θ r = 3 cos ⁡ θ

Igualando as equação teremos o valor de θ

1 + cos ⁡ θ = 3 cos ⁡ θ

3 cos ⁡ θ - cos ⁡ θ = 1

2 cos ⁡ θ = 1

cos ⁡ θ = 1 2

θ = π 3           o u             θ = 5 π 3

Passo 2

Agora vamos começar os nossos cálculos e uma forma de simplificarmos nossas contas é olhar apenas para a parte da região acima do eixo x , pois a área é simétrica. Então no final basta multiplicar a resposta por 2 e teremos a área total.

Para θ no intervalo π 3 ≤ θ ≤ π :

A área da curva de fora será

A f o r a = 1 2 ∫ π 3 π 1 + cos ⁡ θ 2   d θ

Resolvando o produto notável 1 + cos ⁡ θ 2

A f o r a = 1 2 ∫ π 3 π 1 + 2 cos ⁡ θ + cos 2 ⁡ θ   d θ

Sabemos a relação trigonométrica

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2  

Logo,

A f o r a = 1 2 ∫ π 3 π 1 + 2 cos ⁡ θ + 1 + cos ⁡ 2 θ 2   d θ

A f o r a = 1 2 ∫ π / 3 π 3 2 + 2 cos ⁡ θ + cos ⁡ 2 θ 2   d θ

A f o r a = 1 2 ∫ π 3 π 3 2   d θ + ∫ π 3 π 2 cos ⁡ θ   d θ + ∫ π 3 π cos ⁡ 2 θ 2   d θ  

Portanto,

A f o r a = 1 2 3 2 θ + 2   s e n   θ + 1 4 s e n   2 θ π / 3 π

Substitundo os limites de integração

A f o r a = 1 2 3 2 π - π 3 2   s e n   π   - 2 s e n π 3 + 1 4 s e n   2 π - 1 4 s e n 2 π 3

A f o r a = 1 2 π - 3 - 3 8 = π 2 - 9 3 16

Passo 3

Agora vamos achar a área da região da curva de dentro. Nesse caso, θ vai de π 3 até π 2 :

A d e n t r o = 1 2 ∫ π 3 π 2 9 cos 2 ⁡ θ   d θ

Sabemos a relação trigonométrica

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2  

Temos

A d e n t r o = 9 4 ∫ π / 3 π / 2 1 + cos ⁡ 2 θ   d θ

Logo,

A d e n t r o = 9 4 θ + 1 2 s e n   2 θ π 3 π 2

Substituindo os limites de integração.

A d e n t r o = 9 4 π 2 - π 3 + 1 2 s e n   2 . π 2 - 1 2 s e n 2 π 3

Portanto,

A d e n t r o = 9 4 π 6 - 3 4

A d e n t r o = 3 π 8 - 9 3 16

Passo 4

A área que queremos achar é:

A = 2   A f o r a - A d e n t r o

A = 2   π 2 - 9 3 16 - 3 π 8 - 9 3 16

Portanto,

A = 2   π 2 - 3 π 8 2 ⋅ π 8

Assim,

A = π 4

Resposta

A = π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as áreas das regiões nos Exercícios 1-8Dentro do limaçon oval r = 4 + 2 cos ⁡ θ
Encontre os comprimentos das curvas nos exercícios 21-28.A curva r = a s e n 2 θ 2 ,0 ≤ θ ≤ π ,a0 .
Encontre os comprimentos das curvas nos exercícios 21-28.A curva r = cos 3 ⁡ θ / 3 ,0 ≤ θ ≤ π / 4 .
A área da região que está dentro da curva cardioide r = cos ⁡ θ + 1 e fora do circulo r = cos ⁡ θ não é 1 2 ∫ 0 2 π cos ⁡ θ + 1 2 - cos 2 ⁡ θ d θ = π Por que não? Qual é a área? Justifique suas respos
Encontre as áreas das regiões nos Exercícios 9-18Dentro da lemniscata r 2 = 6 cos ⁡ 2 θ e fora do círculo r = 3 .