Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 42
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de em função de nas coordenadas cartesianas.
Passo 1
Para o gráfico podemos iniciar calculando o valor de para diferentes . Sendo assim,
Para
Para
Para
Para
Para
Para
Passo 2
Com esses pontos, é possível plotar um gráfico.
Mas antes disso vamos analisar a equação polar.
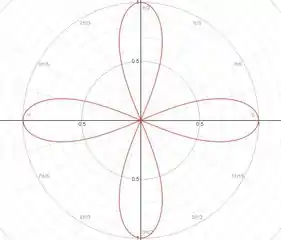
O argumento do cosseno é e isso nos diz que a curva tem a forma de uma flor com4 pétalas, contida dentro de um círculo com raio centrado na origem. O número de pétalas da curva é determinado pelo número de vezes que a função atravessa o eixo no intervalo de a .
A curva é simétrica em relação ao eixo .
De acordo com os valores de , o máximo valor do raio é 1. Sendo assim os pontos mais distantes da origem ocorrem onde , ou seja, nos pontos onde .
Passo 3
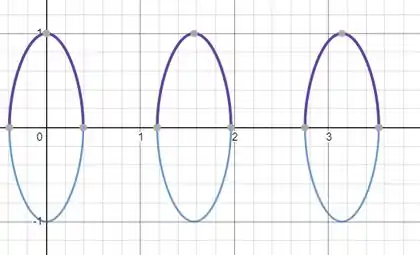
Agora temos que analisar a equação polar em coordenadas cartesianas.
Vamos nos divertir substituindo a equação !!!
Sabemos que
A equação acima representa o gráfico em coordendas cartesianas, esta curva não depende dos sinais de e . E o ponto de máximo ocorre onde , resultando em um círculo com raio centrado na origem, note que não há pontos de mínimo, pois nunca é menor que .
Resposta
A equação polar descreve uma curva com quatro pétalas, simétrica em relação ao eixo , contida dentro de um círculo de raio centrado na origem. Em coordenadas cartesianas, a curva assume a forma de uma flor com características semelhantes, simétrica em relação aos eixos e , com pontos mais distantes da origem formando um círculo de raio .
Moleza neh? Até a próxima!