Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.5 - Ex. 5
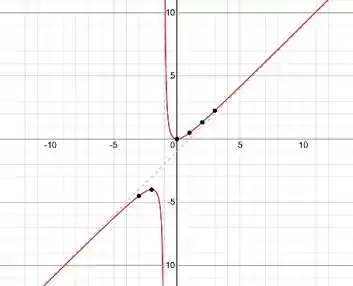
Esboce o gráfico.
Passo 1
Primeiro vamos determinar o domínio, temos aqui que é .
Agora vamos achar os intervalos de crescimento e decrescimento, vamos usar a regra do polinômio, da função constante e da divisão para achar :
Vamos então aplicar:
Passo 2
Agora vamos analisar o sinal de :
Vamos analisar o sinal da expressão:
Para temos:
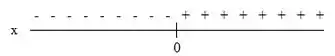
A expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
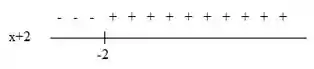
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 3
Vamos lá, agora vamos analisar as duas imagens que achamos no passo anterior:
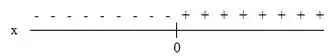
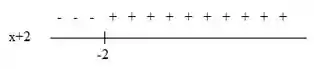
Temos que em:
e
E temos um ponto de descontinuidade em , assim:
e
Como é contínua temos que:
é estritamente crescente em e
é estritamente decrescente em e
Passo 4
Vamos achar os pontos de inflexão e como se comporta a concavidade através de :
em , tendo a concavidade voltada para cima, e em , tendo a concavidade voltada para baixo.
O ponto de inflexão é em , pois nesse ponto não existe.
Passo 5
Para esboçar o gráfico vamos calcular os limites de para e :
Passo 6
Pronto, agora podemos esboçar o gráfico, ficando desse jeito:
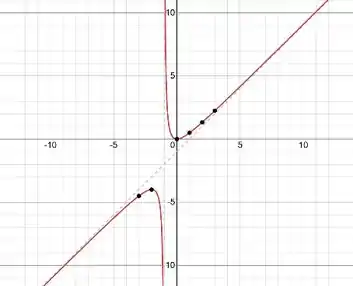
Resposta
