Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.5 - Ex. 15
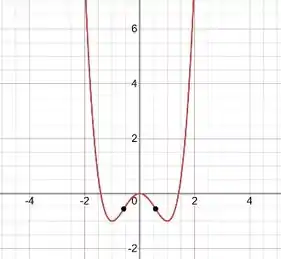
Esboce o gráfico.
Passo 1
Primeiro vamos determinar o domínio, temos aqui que é .
Agora vamos achar os intervalos de crescimento e decrescimento, vamos usar a regra do polinômio para achar :
Vamos então aplicar:
Passo 2
Agora vamos analisar o sinal de igualando a zero:
Vamos analisar o sinal da expressão:
Para temos:
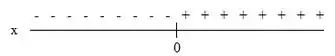
A expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
A expressão assume valores negativos quando e assume valores positivos quando .
E para temos:
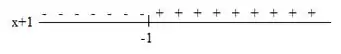
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 3
Vamos lá, agora vamos analisar as três imagens que achamos no passo anterior:
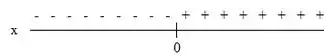
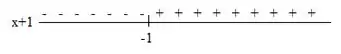
Temos que em:
e
E em:
e
Como é contínua temos que:
é estritamente crescente em e
é estritamente decrescente em e
Passo 4
Vamos achar os pontos de inflexão e como se comporta a concavidade através de :
Igualando a :
Vamos analisar agora o sinal de :
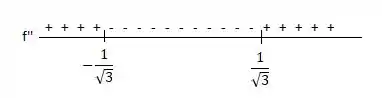
em e , tendo a concavidade voltada para cima, e em , tendo a concavidade voltada para baixo.
Os pontos de inflexão são em e , pois nesses pontos há uma mudança de concavidade.
Passo 5
Para esboçar o gráfico vamos calcular os limites de para e :
Passo 6
E por último vamos achar as raízes de :
Temos como raiz real:
,
Pronto, agora podemos esboçar o gráfico, ficando desse jeito:
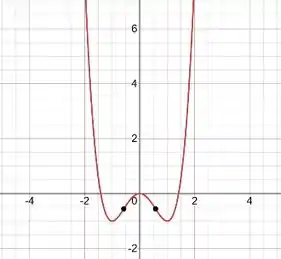
Resposta
