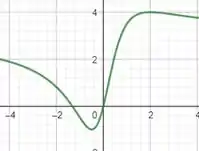
Esboce o gráfico.

Vamos determinar agora os intervalos onde essa função é crescente e onde ela é decrescente. Para isso precisamos calcular a derivada desse carinha

Lembrando que nessa continha usamos a regra da divisão!

O denominador sempre será positivo, então basta olhar o sinal do numerador. Como é uma equação do segundo grau temos que resolver que nem lá no ensino médio

Ou ou .

Podemos usar a seguinte fatoração

Então finalmente a nossa derivada fica

Agora podemos olhar os sinais!

Quando , temos que e . Como a expressão tem um sinal de menos na frente vamos ter que para , , ou seja, a função é decrescente nesse intervalo.

Quando , temos que e . Como a expressão tem um sinal de menos na frente vamos ter que para , ou seja, a função é crescente nesse intervalo.

Quando , temos que e . Como a expressão tem um sinal de menos na frente vamos ter que para , ou seja, a função é decrescente nesse intervalo.

Agora vamos olhar a concavidade da curva. Pra isso precisamos da derivada segunda da função!

De novo vamos usar a regra da divisão! As derivadas separadas do numerador e do denominador são

Juntando isso tudo

E se igualarmos o numerador a chegamos numa equação que não conseguimos resolver! ☹

Mas jogando na calculadora vemos que a derivada segunda se anula para

Nesses dois valores, o nosso gráfico terá uma inflexão! Chutando alguns valores pra esse numerador também podemos afirmar que:

para convexa

para côncava

para convexa

Agora vamos olhar os limites de

E por últimos vamos olhar as raízes da nossa função. Isso acontece quando o denominador é nulo, ou seja,

Ou

E essas são as raízes da nossa função!

Juntando todas essas informações podemos fazer o seguinte esboço:

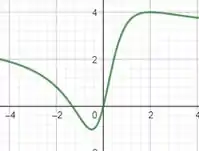
Prontinho!!!