Esboce o gráfico da função racional:
Passo 1
Primeiramente, vemos que o domínio da função é (não pode zerar o denominador)
Vamos calcular a derivada primeira e segunda:
Passo 2
Vamos encontrar os pontos críticos agora, que são onde a derivada é zero.
Então, a função não apresenta extremos relativos e absolutos.
Veja que a função não está definida para e , mas está definida em todos os pontos próximos a esses. Com isso, temos assíntotas verticais em .
Passo 3
Vamos agora ver os intervalos de crescimento da função.
Vimos que a função não apresenta pontos críticos, mas possui assíntotas, então vamos analisar o sinal da derivada antes e depois das assíntotas:
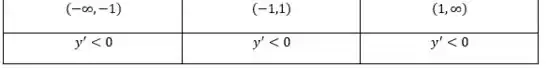
Então, a função é sempre decrescente.
Vejamos a concavidade...
Nossa derivada segunda deu
Vemos que :

Então, a concavidade é para baixo em e para cima em e
A função muda a concavidade em , porém não temos pontos no local já que eles não pertencem ao domínio. Temos um ponto de inflexão em .
Passo 4
Juntando as informações, temos o gráfico:
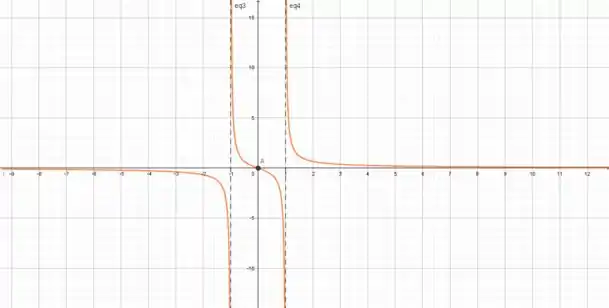
Resposta
Ei, a resposta está no passo a passo :)