Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.2 - Ex. 11b

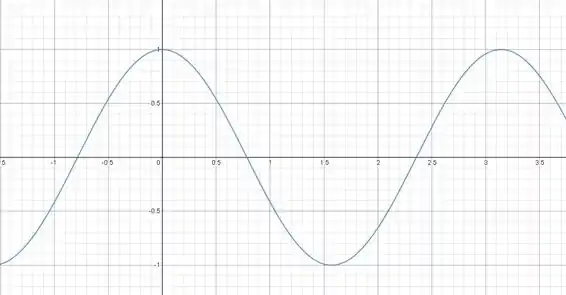
Esboce o gráfico da função y = y (x) , x in R , Sabendo que

b ) (d^2 y)/(d x^2) = - 4 cos 2 x , y (0) = 1 e y ' (0) = 0

Passo 1

Sendo a segunda derivada:

(d^2 y)/(d x^2) = - 4 cos 2 x

Ou seja, a primitiva de (d^2 y)/(d x^2)

(d y)/(d x) = int - 4 cos 2 x d t

Usando a substituição u = 2 x -> d u = 2 x d x , teremos:

- 4 xx (1)/(2) int cos u d u = - 2 sin u + k

Voltando pra variável x :

- 2 s in u + k = - 2 s in 2 x + k

Passo 2

Agora precisamos de k

(d y)/(d x) = - 2 s in 2 x + k

Pra isso vamos usar x = 0

(d y)/(d x) (0) = - 2 sin 2 (0) + k = 0 + k = k

O exercício nos deu que (d y)/(d x) (0) = 0 , então igualamos:

v (0) = 0 = k -> k = 0

Assim:

(d y)/(d x) = - 2 s in 2 x

Passo 3

Se (d y)/(d x) = - 2 sin 2 x

Então:

y (x) = int (- 2 sin 2 x) d x

Vamos usar, novamente, a substituição u = 2 x -> d u = 2 d x

int (- 2 sin 2 x) d x = (1)/(2) int (- 2 s in u) d u = [cos u] + c

Voltando pra variável x :

[cos 2 x] + c = cos 2 x + c

Assim:

y (x) = cos 2 x + c

y (0) = cos 2 (0) + c = c

E y (0) = 0

Assim, se igualarmos os valores de y (0) , teremos:

0 = c

Logo:

y (x) = cos 2 x

Assim, vamos ter uma função cos x porém 2 vezes menos espaçado, assim:

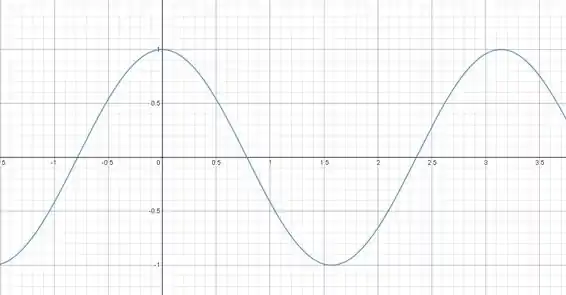
Repare nesse desenho comparando as funções y = cos x e y = cos 2 x

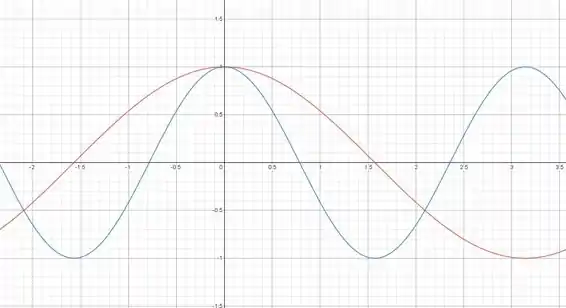
Repare que tem uma que demora bem mais pra passar no eixo x

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula desloca-se sobre o eixo 0 x , de modo que em cada instante t a velocidade é o dobro da posição x = x t . Sabe-se que x 0 = 1 . Determine a posição da partícula no instante t .
A função y = f x , x ∈ R , é tal que f 0 = 1 e f ' x = - 2f x para todo x . Esboce o gráfico de f .
Calculeu)int (2 + s e n ((x)/(3))) d x
Calculeq)int (x + e^(3 x)) d x
Calculet)int (1 - cos (4 x)) d x