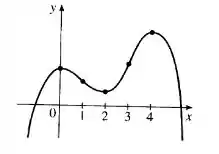
Esboce o gráfico de uma função que satisfaça todas as condições dadas.
se ou ,
se ou ,
se , se ou
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão pediu pra gente esboçar o gráfico de uma função que satisfaça a algumas condições.
Vamos analisar cada uma dessas condições e entender como elas influenciam no gráfico da nossa função.
Essa condição fala que nesses pontos a derivda tem que ser igual a zero. Então devemos lembrar que a derivada é igual a inclinação da reta tangente ao gráfico da função.
Isso significa que teremos um ponto de máximo ou mínimo da função nesses lugares.
se ou ,
Nessa condição estamos falando de uma região onde a reta tangente possui inclinação positiva. Sendo assim, teremos uma função crescente nesses interevalos sitados.
se ou ,
Aqui temos o caso contrário, regiões onde a derivada é negativa indicarão uma região onde a função é decrescente.
E
se
se ou
A derivada segunda ajuda a gente a classificar os pontos críticos de acordo com a concavidade da função na região. Veja:
![]()
Prontinho. Agora que já sabemos como cada condição infuencia no gráfico, vamos ver como fica nossa resolução.
Passo 2
Vamos analisar cada informação dada então. Veja:
Se
Então possui retas tangentes horizontais em , e .
Como
se ou
Então é crescente para valores de menores que zero ou entre e .
Como
se ou
Então é decrescente para valores de maiores que ou entre e .
Passo 3
Como
se
então possui concavidade voltada para cima para valores de entre e .
Como
se ou
Então possui concavidade voltada para baixo para valores de menores que ou maiores que .
Passo 4
Com essas informações, temos o gráfico:
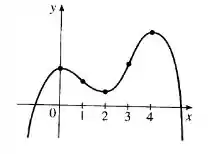
Resposta