Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 6
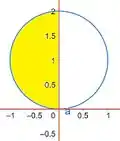
Esboce a região cuja área é dada pela integral e calcule-a.
Passo 1
E aiiiii minha turminha, tudo bem? Vamos lá!
A questão nos fornece uma integral dupla iterada, ou seja, com intervalos de integração. E partir disso devemos esboçar a região de integração e calcular o valor da integral.
Como vamos fazer isso?
A parte de calcular o valor da integral é a mais fácil desta questão. Pois já está em coordenadas polares, então basta vocês começarem a integrar a função de dentro para fora e aplicar os limites de integração.
Agora, o esboço da região vamos com calma, beleza!
Para esta nossa questão, o valor do raio varia de até . Para facilitar a identificação do esboço, a função pode ser transformada novamente para coordenadas cartesianas. Sabemos que:
Sabemos do problema que: .
O objetivo é manipular essas equações e determinar a equação do círculo, que vai ficar com essa cara:
Como nosso ângulo varia de até , estamos com nossa região no segundo quadrante.
Com esse bizu monstro, bora colocar mão na massa!!!
Passo 2
Vamos começar determinando nossa região.
Já sabemos pelo formato da integral, que se trata de um círculo:
Onde, o raio varia de:
Temos as seguintes coordenadas polares:
Podemos isolar :
E temos que:
Vamos substituir na expressão acima, ficando:
Agora vamos substituir na equação do círculo:
Logo, temos:
Completando quadrados, vamos ter a seguinte expressão:
Observe a expressão. Você concorda que conhecemos essa expressão, que é um círculo de raio que está centrado em e .
Agora, observe na imagem abaixo, e veja como ela reflete o que acabamos de dizer.
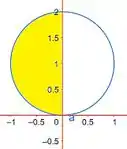
Mas lembra que varia de até , o que corresponde a todo o segundo quadrante.
Passo 3
Agora, vamos resolver a nossa integral.
Integrando em , temos que:
Aplicando os limites de integração, vamos ficar com:
Vamos separar em duas integrais para facilitar:
Na segunda integral, aplicamos uma substituição do tipo:
Logo,
Integrando e voltando para :
Aplicando os limites de integração, vamos ter como resposta:
Resposta
