Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 43
43) Esboce a região de integração e mude a ordem de integração
Passo 1
Falaaaiiii, vamo lá resolver essa questão?! Simbora! Queremos esboçar a região que estamos integrando, certo?! Então beleza, vamos analisar os intervalos de integração, pois nossa região é dada por eles!! Do enunciado:
Sendo assim, nossa região D, será:
Agora vamos interpretar isso
Passo 2
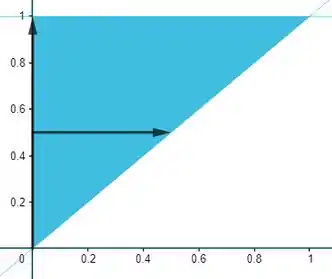
Pra começar, vamos ver o intervalo de :
Po galera, isso quer dizer que o sai do eixo (onde ) e toca o a reta x. Seria esse intervalo aqui ó:
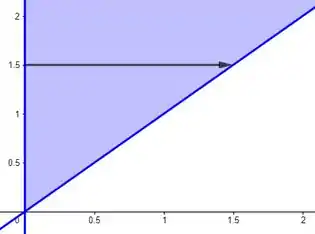
Pro intervalo de , temos:
O que nada mais é do que esse intervalo aqui:
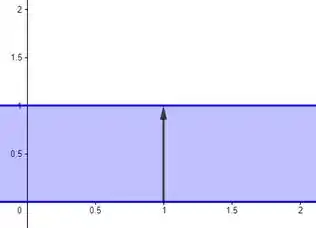
A região vai ser então a união desses dois azuiszinhos:
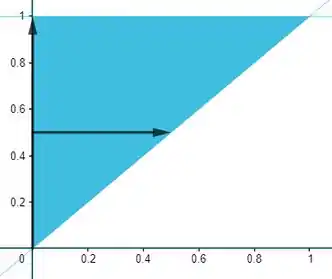
Passo 3
Pra fazer a mudança de ordem de integração temos que partir do mesmo :
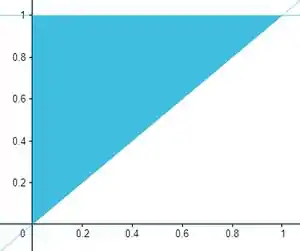
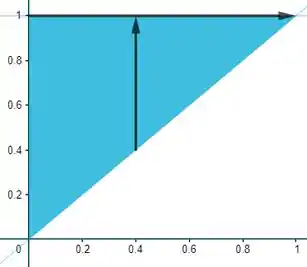
E trocar a ordem das setas, beleza? Bem, se antes tínhamos o delimitado por um número e uma função (), agora teremos o delimitado. Note que pra gente escolher o intervalo podemos ver aqui que:
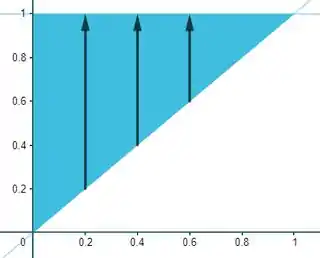
O sempre sai da reta e vai até a horizontal . Sendo assim, o intervalo será:
Por outro lado, o triângulo que é a região está inteiramente definido entre dois intervalos de , que são:
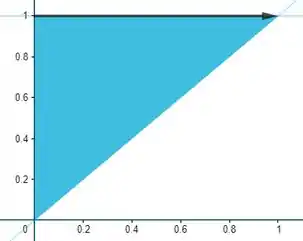
Então, invertendo a ordem de integração, temos:
Daí, nossa região será:
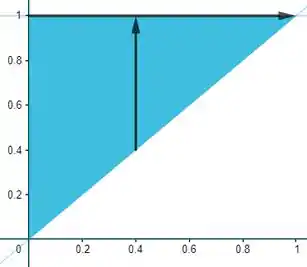
E a sua integral correspondente:
Feshow!
Resposta
