Estime o valor de usando uma tabela de valores para para conjecturar o valor do limite. Demonstre que sua conjectura está correta.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui queremos encontrar o valor do limite da função dada por 2 caminhos, primeiro iremos criar uma tabela para os valores de , onde iremos colocar valores cada vez maiores e iremos ver para onde a função nos leva. Depois disso iremos provar que estamos certos, agora realmente resolvendo o limite.
Passo 2
Para demonstrar que está correto, iremos calcular o limite de forma algébrica. Porém, como é um limite no infinito, devemos mexer algebricamente na função de forma a tentar facilitar nossa vida, pois não podemos simplesmente trocar por .
Seja , multiplicaremos tudo pelo conjudado, tal que o conjugado vale 1, então
Então, ficamos com
Agora, dividiremos em cima e em baixo pelo denominador de maior potência, no caso, para que possamos anular o termo quando .
Daí, temos
Note que o sinal negativo apareceu no denominador, pois é menor que zero, logo , então ao dividirmos pelo denominador de maior potencia ficamos com,
Passo 3
Agora, aplicaremos o limite na que encontramos, porém precisamos lembrar de duas coisas, a primeira é que e a segunda é que , então,
Passo 4
Agora iremos aqui criar a nossa tabela de valores.
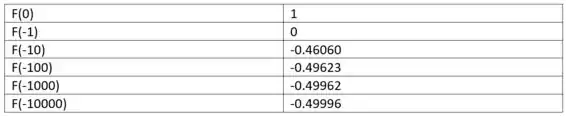
Podemos ver que o valor que encontramos é de fato o valor para o qual a função caminha.