Exercícios de Indeterminação Infinito - Infinito - Lista de Exercícios Resolvida
Questão 17
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 18
Classifique os limites abaixo agora usando a noção generalizada que inclui ou como resposta.
Ver solução completaQuestão 19
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 20
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 21
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 22
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 23
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 26
Calcule os seguintes limites (não é permitido o uso da regra de l’Hôspital):
Ver solução completa
Questão 27
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 28
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 32
Sejam e funções polinomiais. Baseado nos exercícios já resolvidos, formule um teorema que indique o resultado dos limites e
Ver solução completaQuestão 33
As definições limites no infinito possuem versões formais semelhantes às que vimos para o limite usual. Tente formular uma definição precisa para todos os tipos de limites no infinito e depois pesquise se sua definição está correta.
Ver solução completaQuestão 34
Classifique os limites abaixo agora usando a noção generalizada que inclui ou como resposta.
Ver solução completaQuestão 37
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 39
- Nesse exercício, vamos revisitar alguns limites que já apareceram em listas anteriores. Como agora temos à disposição a noção de limites infinitos, podemos nos perguntar se limites que antes eram classificados como agora podem ser classificados como ou . Classifique os limites abaixo agora usando a noção generalizada que inclui ou como resposta.
b.
Ver solução completaQuestão 40
Classifique os limites abaixo agora usando a noção generalizada que inclui ou como resposta.
Em que é a função cujo gráfico é dado abaixo:
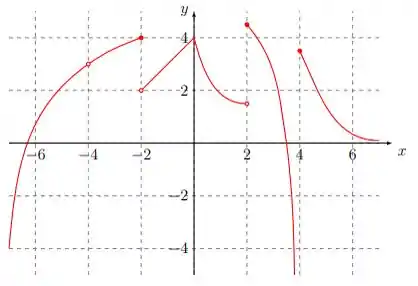
Questão 41
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 42
- Nesse exercício, vamos revisitar alguns limites que já apareceram em listas anteriores. Como agora temos à disposição a noção de limites infinitos, podemos nos perguntar se limites que antes eram classificados como agora podem ser classificados como ou . Classifique os limites abaixo agora usando a noção generalizada que inclui ou como resposta.
Ver solução completaQuestão 46
1b) Calcule ou justifique caso não exista, cada um dos limites abaixo
Ver solução completaQuestão 47
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Obs: considere
Ver solução completaQuestão 49
Mostre que toda função polinomial de grau ímpar possui pelo menos uma raiz real. Ao final de sua demonstração, explique por que o mesmo argumento não funciona para funções polinomiais de grau par. Sugestão. Seja uma função polinomial de grau ímpar. Utilize seus conhecimentos de limite para mostrar que e ou que e . Com esse resultado, utilize o significado de limite para concluir a existência de tais que e : Por fim, aplique um teorema visto nas aulas para concluir o resultado.
Ver solução completaQuestão 50
11.5 Calcule os limites abaixo de forma detalhada e sem usar o Teorema de L’Hospital:
a)
Ver solução completaQuestão 51
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 52
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 53
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 60
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 84
1.2. A resolução abaixo está INCORRETA. Indique onde ocorrem os erros e então calcule o limite correta.
Ver solução completaQuestão 85
Dizemos que duas funções reais f e g, são equivalentes se . Indicamos isso escrevendo f ∼ g. Qual das afirmações abaixo NÃO é consequência de f ∼ g?
a. ; b. ; c. ; d. ; e. .
Ver solução completaQuestão 98
Explique o significado das expressões ”indeterminadas”abaixo e exemplifique esta situação:
(a) Produtos Indeterminados
(b) Diferenças Indeterminada
(c) Potências Indeterminadas
Ver solução completaQuestão 99
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 100
Calcule os limites abaixo, se existirem, usando a generalização de limites infinitos
Ver solução completaQuestão 109
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando ou apresentando um contra-exemplo.
a. Se f , g : R → R são funções tais que f é limitada e positiva e , então tem-se que .
b. Se f , g : R → R são funções tais que f é limitada e , então tem-se que .
c. Se f , g : R → R são funções tais que , então .
Ver solução completaQuestão 110
Considere a afirmação “Sejam funções tais que e é limitada. Então ”. É correto dizer
- Tal afirmação é verdadeira
- Tal afirmação é verdadeira se supomos que
- Tal afirmação é verdadeira se supomos que exista algum tal que para todo
- Tal afirmação é verdadeira se supomos que exista algum tal que para todo
- Tal afirmação é falsa para toda limitada
Questão 125
9. Calcule o limite, caso exista, os especifique porque não existe. Não é permitido usar derivada. Lembre-se de justificar sua resposta.
a)
b)
Ver solução completa