Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.2 - Ex. 18
Nos exercícios de 15 a 20, faça o seguinte:
- Use uma calculadora para tabular, até quatro casas decimais, os valores de para os valores fixados de . Do que parece tender quando se aproxima de
- Encontre o ache o e, quando aplicável, indique os teoremas de limite usados.
Passo 1
Na letra a precisamos achar para os valores de dados. Feito isso, devemos observar de quais valores quando o nosso está se aproximando de . Isso nos dará o limite calculado diretamente pela função. Já na letra b iremos comprovar esse resultado resolvendo pelos teoremas.
Para resolver a letra a vamos fazer duas tabelas com os valores de e
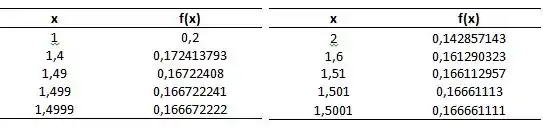
Quando se aproxima de , se aproxima de 0,1667.
Agora devemos calcular o limite pelos teoremas para comprovar o resultado obtido diretamente.
Passo 2
Para a letra b devemos resolver:
Podemos resolver o limite usando o Teorema de Limite 9:
Sendo assim:
Usando o Teorema 1:
Pelo Teorema 2:
Concluindo:
Resposta
- 0,1667
Exercícios de Livros Relacionados
74. Seja G ( t ) = ( 1 - cos t ) / t 2 .a. Faça uma tabela dos valores de G em valores de t que se aproximam de t 0 = 0 por cima e por baixo. Em seguida, estime lim t → 0 G ( t ) b. Apoie suas con
A figura a seguir mostra o gráfico da distância em função do tempo da queda de um objeto que caiu do módulo lunar a uma distância de 80m da superfície da Lua.Estime os coeficientes angulares das secan
Faça uma tabela de valores para a função F x = ( x + 2 ) / ( x - 2 ) nos pontos x = 1,2 , x = 11 / 10 , x = 101 / 100 , x = 1001 / 1000 , x = 10001 / 10000 e x = 1 .Determine a taxa média de variação
O gráfico a seguir mostra a quantidade total de gasolina A no tanque de combustível de um automóvel que rodou por t dias.Estime a taxa média do consumo de gasolina nos intervalos 0 ; 3 ,0 ; 5 e 7 ; 10
Velocidade de um carro A figura a seguir ilustra o gráfico da distância em função do tempo para carros esporte que aceleram a partir do repouso.Estime os coeficientes angulares das secantes P Q 1 , P