Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.1 - Ex. 17

Nos Exercícios 15-18, utilize uma soma finita para estimar o valor médio de f no intervalo dado, dividindo-o em quatro subintervalos de comprimento igual e avaliando f nos pontos médios dos subintervalos.

17. f t = 1 2 + sen 2 ⁡ π t em 0 ,   2

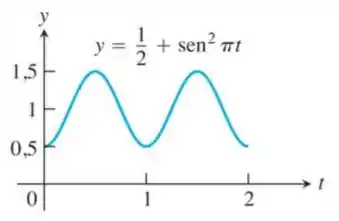
Passo 1

Vamos dividir f em 4 subintervalos: 0 ; 0,5 ,   0,5 ; 1,0 ,   1,0 ; 1,5   e   1,5 ; 2,0 . Seus pontos médios são: m 1 = 0,25 ; m 2 = 0,75 ; m 3 = 1,25   e m 4 = 1,75 , respectivamente.

Passo 2

Agora precisamos achar a altura que cada retângulo terá, para isso vamos aplicar os valores dos pontos médios na função:

1:

f 1 ( 0,25 ) =   1 2 + sen 2 ⁡ ( π ⋅ 0,25 )

f 1 0,25 =   1 2 + 2 2 2

f 1 0,25 =   1 2 + 1 2

f 1 0,25 = 1

2:

f 2 ( 0 , 7 5 ) =   1 2 + sen 2 ⁡ ( π ⋅ 0 , 7 5 )

f 2 0 , 7 5 =   1 2 + 2 2 2

f 2 0 , 7 5 =   1 2 + 1 2

f 2 0 , 7 5 = 1

3:

f 3 1 , 25 =   1 2 + sen 2 ⁡ ( π ⋅ 1 , 25 )

f 3 1,25 =   1 2 + - 2 2 2

f 3 1,25 =   1 2 + 1 2

f 3 1,25 = 1

4:

f 4 1 , 7 5 =   1 2 + sen 2 ⁡ ( π ⋅ 1 , 7 5 )

f 4 1,75 =   1 2 + - 2 2 2

f 4 1,75 =   1 2 + 1 2

f 4 1,75 = 1

Passo 3

Para acharos a área total só precisamos somar a área dos 4 retângulos. Como suas bases e suas alturas são iguais, podemos escrever que:

Á r e a = 4 ⋅ b a s e ⋅ a l t u r a

Á r e a = 4 ⋅ 0,5 ⋅ 1

Á r e a = 2

O valor médio da função vale:

V a l o r   m é d i o = Á r e a   s o b   a   c u r v a C o m p r i m e n t o   d a   b a s e

V a l o r   m é d i o = 2 2

V a l o r   m é d i o = 1

Resposta

V a l o r   m é d i o = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ