Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.
6 -
Passo 1
Primeiramente char K:
teremos:
Resolvendo e achando:
Passo 2
Utlizando a função:
Assim:
Logo:
Integrando:
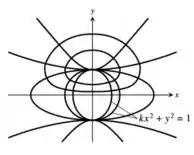
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.
6 -
Primeiramente char K:
teremos:
Resolvendo e achando:
Utlizando a função:
Assim:
Logo:
Integrando:
