Nos Exercícios 61-66, você aprofundará a exploração determinando deltas grafica1nente. Utilize um SAC para executar as seguintes etapas:
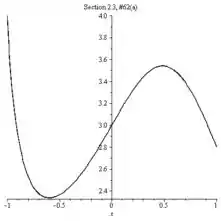
- Trace a função próximo ao ponto sendo aproximado.
- Descubra o valor do limite L e, em seguida, avalie o limite simbolicamente para verificar se está correto.
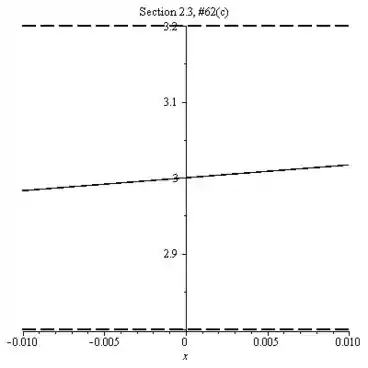
- Utilizando o valor , faça o gráfico das retas e , juntos com a função de f próxima a
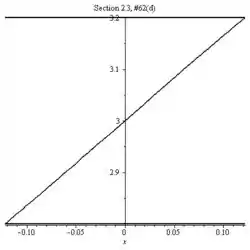
- A partir do seu gráfico no item (c), estime um de modo que para todo x:
- Repita os itens (c) e (d) sucessivamento para
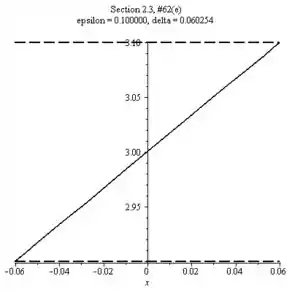
Teste a sua estimativa traçando f, e no intervalo . Para sua janela de inspeção utilize e . Se algum valor da função estiver fora do intervalo , sua escolha de foi alta demais, tente novamente com uma estimativa menor.
62 - .
Passo 1
Neste exercício utilizaremos o maple, desta forma segue os comandos que deverão ser digitados no software:

Alguns comandos básicos foram apresentados na solução do exercício anterior.
Logo após aplicar estes códigos no software, teremos os seguintes resultados:
![]()
![]()
![]()
![]()
![]()
![]()
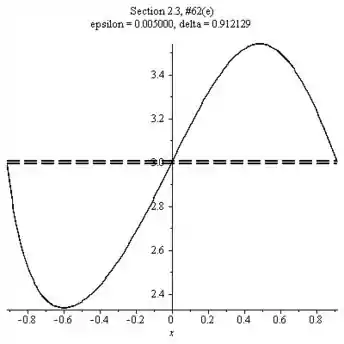
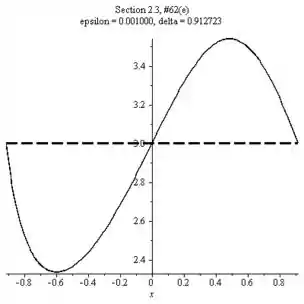
Resposta
Ei, a resposta está no passo a passo :)