Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.3 - Ex. 14
Nos Exercícios 7-14, utilize os gráficos para determinar um e que para todo
14.
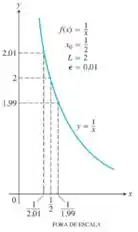
Passo 1
Basicamente, nós precisamos achar um valor de que faça com que seja sempre valido.
O gráfico nos mostra que , se substituirmos esse valor na inequação, vamos obter:
Vamos precisar uma regrinha das inequações agora, a expressão vai ficar:
Então o pode ficar entre o intervalo de
Passo 2
Mas nós também sabemos, pelo gráfico, que o está no intervalo:
Então podemos escrever que:
Agora só precisamos resolver as equações para descobrirmos um valor valido para :
Resolvendo a outra equação:
Precisamos pegar o menor valor do , pois podemos usar ele tanto para esquerda quanto para a direita.
Já se escolhermos o maior nesse caso, ele vai valer para o lado direito mas no lado esquerdo vai fazer com que .
Portanto