Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.7 - Ex. 33
Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados.
na placa triangular fechada e limitada pelas retas , , no primeiro quadrante.
Passo 1
Oi pessoal, tudo bem com vocês? Vem comigo, que vou te explicar este exercício no passo a passo.
Para determinarmos os valores máximo e mínimo absolutos de uma função contínua em um conjunto fechado limitado :
- Determine os valores de nos pontos críticos de em .
- Determine os valores extremos de na fronteira de .
- O maior dos valores dos pontos (a) e (b) é o valor máximo absoluto; o menor desses valores é o valor mínimo absoluto.
Sendo assim, primeiro temos que encontrar os pontos críticos da função, que descobrimos pelas derivadas parciais de primeira ordem, da função dada no enunciado:
Quando essas derivadas são nulas, temos o sistema com duas equações e duas incógnitas:
Da equação (I), temos:
E na equação (II):
Sendo assim, o único ponto crítico existente é . O valor de neste ponto é:
Passo 2
No ponto (b), consideramos um lado do triângulo de cada vez, que é constituído por 3 segmentos de reta , e , de acordo com a Figura:
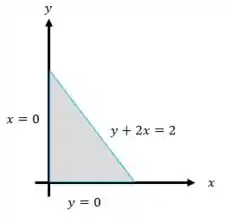
Em , temos . A função:
na placa triangular fechada e limitada pelas retas , , no primeiro quadrante.
Pode ser considerada uma função definida no intervalo fechado . Seus valores extremos podem ocorrer nas extremidades:
- onde ;
- onde .
- ;
- .
E nos pontos interiores onde , o único ponto interior é:
Que é o mesmo ponto encontrado anteriormente .
Passo 3
No segmento , temos :
Sabemos pela simetria de em e , e que , que os candidatos nesse segmento são:
Passo 3
Já levamos em consideração os valores de nas extremidades de , assim precisamos somente examinar os pontos interiores de . Com , temos:
Fazer , resulta:
Nesse valor de :
Então o ponto é:
Então, agora conseguimos relacionar os candidatos: , , e . O mínimo é , que assume em e o máximo é , que assume em .
Resposta
- Mínimo absoluto: em ;
- Máximo absoluto: em .