Exercícios de Máximos e Mínimos Globais numa Região Fechada - Lista de Exercícios Resolvida

Sejam número real, e .

(a) Classifique os pontos críticos de em função de .

(b) Considere . Encontre os valores máximo e mínimo de no conjunto

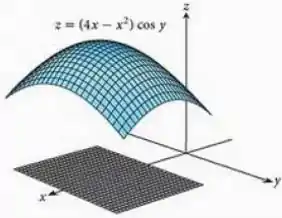
Encontre o máximo e o mínimo absoluto da função

na placa retangular (veja figura a seguir).

Encontre os pontos de máximo e mínimo globais da função dentro de .

Determine os valores máximo e mínimo absolutos de

no conjunto

Seja dada por

1. Determine e classifique os pontos críticos.
2. Determine , caso existam, os pontos de máximo e de mínimo de no conjunto

Determine os valores máximo e mínimo absolutos de

no conjunto

Sejam dada por e

1. Determine todos os pontos críticos de em .

2. Classifique todos os pontos críticos de em .

3. Determine os pontos de máximo e mínimo de na circunferência

4. Determine os pontos de máximo e mínimo de em .

Sejam e , definida no maior domínio possível. A soma das coordenadas do ponto em que , restrita a , atinge seu valor máximo quando?

Encontre os valores máximo e mínimo absoluto da função

no quadrado unitário .

Sejam número real, e .

(a) Classifique os pontos críticos de em função de .

(b) Considere . Encontre os valores máximo e mínimo de no conjunto

Seja

E considere a região triangular, fechada, de vértices . Qual das afirmativas abaixo é verdadeira?

1. O maior valor de em é 1 e o menor valor de em é .
2. O maior valor de em é 2 e o menor valor de em é .
3. O maior valor de em é 9 e o menor valor de em é .
4. não assume um valor máximo em .
5. Nenhuma das demais alternativas.

Determine os valores e os respectivos pontos de máximo e de mínimo da função restrita à elipse

Considere a função e o domínio

Considere as afirmativas:

1. tem dois pontos de máximo absoluto em
2. tem dois pontos de mínimo absoluto em
3. O valor máximo absoluto de em é 1.
4. O valor mínimo absoluto de em é 0.
5. tem apenas um ponto crítico no interior de

Assinale a alternativa correta:

1. Apenas as afirmativas II e IV são falsas
2. Todas as afirmativas são verdadeiras
3. Todas as afirmativas são falsas
4. Apenas a afirmativa IV é falsa
5. Apenas a afirmativa V é falsa

Considere a função definida por

Onde é uma constante real não nula.

1. Encontre os pontos críticos de
2. Determine os pontos de máximo, mínimo e sela da função dada.
3. Faça e determine os valores de máximo e mínimo absolutos de na região compacta

Os valores máximo e mínimo absolutos de

Na região

São, respectivamente:

Determine os valores máximos e mínimo absolutos de

No conjunto

Considere o quadrado

E a função

Definida em .

1. Determine os valores máximo e mínimo de na fronteira de .
2. Determine os valores máximo e mínimo de em .

Encontre o maior e o menor valor de no círculo . Em que pontos tais valores são atingidos?

Suponha que representa o valor da temperatura em sobre os pontos do plano .

1. Determine o ponto de mais baixa temperaura da reta

Determine os pontos de máximo e de mínimo globais da função restrita à elipse

Seja e . Então:

O máximo absoluto de é atingido no interior de

O máximo absoluto de é atingido na fronteira de

não possui mínimo absoluto em

não possui máximo absoluto em

O mínimo absoluto de é atingido no interior de

Seja dada por

1. Determine os pontos críticos de e classifique-os.
2. Determine, se houver, os pontos de máximo e mínimo de restrita ao conjunto

(Capítulo 14.7 – Exercício 29) Determine os valores máximo e mínimo absolutos de no conjunto .

, é a região triangular fechada com vértices , e .

1. Encontre os valores máximo e mínimo absoluto de no conjunto

Considere a função e a região

1. Determine, caso existam, os extremos locais de no interior de

Considere a função e a região

c) Calcule os valores máximo e mínimo absolutos de no domínio .

Considere o quadrado

E a função

Definida em .

1. Determine os valores máximo e mínimo de na fronteira de .
2. Determine os valores máximo e mínimo de em .

Os valores máximo e mínimo absolutos de

Na região

São, respectivamente

Questão 5 – Considere a função

a) Calcule as derivadas parciais de primeira e segunda ordem.

b) Determine os pontos de sela, de máximo e mínimo locais, se existirem, preenchendo a tabela abaixo

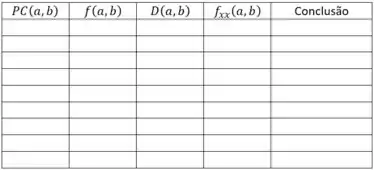
c) Determine os pontos de mínimo e máximo absolutos de na região interna delimitada (fronteira inclusa) pela curva abaixo, cuja equação é .

Seja .

1. Dados os pontos e , decida quais deles são pontos de máximo local, de mínimo local, ou ponto de sela de .
2. Determine os valores de máximo e mínimo de em , em que é a região do plano delimitada pelo retângulo de vértices e .

Seja

1. Determine os pontos críticos de e classifique-os.
2. Determine o máximo e o mínimo de no quadrado (com interior e bordas) cujos vértices são , , e .

Suponha que

represente uma distribuição da temperatura no plano. Determine os pontos da região

de maior e menor temperatura.

Seja a função definida por

Onde D é a região triangular fechada com vértices . Preencha os espaços abaixo:

• O valor máximo absoluto de é :
• O valor mínimo absoluto de é:

2.9. Ache a derivada direcional máxima de no ponto dado e dê a direção em que ela ocorre. a. em ;

b. em .

2 - Encontre o máximo e mínimo globais de cada uma das seguintes funções:

a) , , ;

2 - Encontre o máximo e mínimo globais de cada uma das seguintes funções:

c) , , .

(1) Ache pontos de máximo e mínimo globais de sujeita à restrição

Seja é uma função diferenciável num ponto . Se , .... afirmar que é um ponto de mínimo ou de máximo local de .

Considere a função .

1. Determine os pontos críticos e classifique-os.
2. Determine os pontos de máximo e mínimo absolutos da função sobre o conjunto compacto .

Sejam e , dada por . Se e são, respectivamente, os valores máximo e mínimo globais de em , então:

Sejam e dada por . Se e são, respectivamente os valores mínimo e máximo de sobre , então:

não admite pontos de máximo e mínimo sobre C

Seja definida na região triangular fechada com vértices e . Qual das afirmativas abaixo é verdadeira?

1. O máximo absoluto de em é e o mínimo absoluto de em é
2. O máximo absoluto de em é e o mínimo absoluto de em é
3. O máximo absoluto de em é e o mínimo absoluto de em é
4. O máximo absoluto de em é e o mínimo absoluto de em é
5. Não sei

Determine os valores de a para os quais a função

c. Existe a ∈ R para o qual a função tenha ao menos um máximo local?

Determine os valores de a para os quais a função

b. tenha exatamente dois pontos de sela e um mínimo local;

Identifique os pontos de máximo e mínimo globais da função na região