Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 31
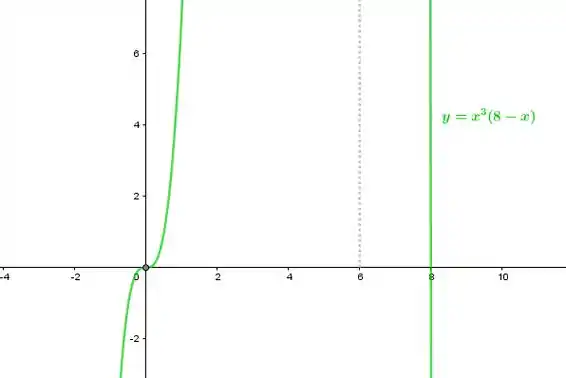
Faça o gráfico da curva
Passo 1
Inicialmente vamos considerar e observar o que essa função tem a nos “dizer”.
Observe que o domínio de corresponde ao conjunto dos números Reais, isso porque não há nenhum valor para que apresente indeterminações ou fatos inexistentes. (raízes quadradas negativas, logaritmos de números negativos, entre outros...)
Sendo assim, o gráfico de não está limitado dentro de nenhum intervalo.
Passo 2
Em seguida verificaremos, se possui raízes, ou seja, se o gráfico toca o eixo
Com isso percebemos que para e temos que ou seja,
E,
Logo, o gráfico de toca o eixo duas vezes.
Passo 3
Determinaremos agora e , para em seguida verificarmos se possui máximos, mínimos ou pontos de inflexão. Dessa maneira temos que,
Pela regra do Produto,
Calculando a segunda derivada utilizando a regra da diferença
Passo 4
Vamos agora identificar se possui pontos críticos
Em relação aos pontos de inflexão temos que
ou
Sendo assim temos dois candidatos à pontos críticos, vamos verificar se qual a mudança de sinal nas proximidades de cada um deles.
Perceba que , para valores dentro do intervalo , assume valores positivos (crescente). E para valores dentro do intervalo , irá assumir valores positivos (cresecente). Logo, não é nem um ponto de máximo nem de mínimo no intervalo de
Perceba que para valores próximos de pela esquerda irá assume valores negativos (decrescente). Já para valores próximos de pela direita, irá assumir valores positivos (crescente). Logo, não assume nem máximo e nem mínimo.
Já, para valores próximos de pela esquerda irá assume valores positivos (crescente). E para valores próximos de pela direita, irá assumir valores negativos (decrescente). Logo, assume um máximo em .
Passo 5
Vamos agora identificar se possui pontos de inflexão
Em relação aos pontos de inflexão temos que
ou
Sendo assim temos dois candidatos a ponto de inflexão, vamos verificar se há mudança de sinal nas proximidades de cada um deles.
Perceba que para valores próximos de pela esquerda irá assume valores negativos (concavidade para baixo). Já para valores próximos de pela direita, irá assumir valores positivos (concavidade para cima). Logo, há mudança de sinal.
Já, para valores próximos de pela esquerda irá assume valores positivos (concavidade para cima). E para valores próximos de pela direita, ainda irá assumir valores positivos (concavidade para cima). Logo, não há mudança de sinal.
Sendo assim, é um ponto de inflexão para , ou seja, há uma mudança de concavidade em
Passo 6
Para finalizar verificaremos se possui assíntotas verticais ou horizontais.
No que se refere as assíntotas horizontais temos que
Logo, não possui assíntotas horizontais.
No que se refere as assíntotas verticais, não há nenhum ponto no domínio de que faça com que
Logo, não possui assíntotas verticais.
Resposta
