Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 60
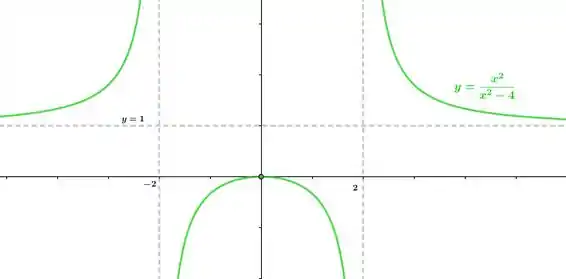
Faça o gráfico da curva
Passo 1
Inicialmente vamos considerar e observar o que essa função tem a nos “dizer”.
Observe que o domínio de corresponde ao conjunto dos números Reais, exceto por , já que quando substituímos esse valor na função acontece uma divisão por zero, que é uma indeterminação matemática.
Sendo assim, o gráfico de está definida para todo
Passo 2
Em seguida verificaremos, se possui raízes, ou seja, se o gráfico toca o eixo
Para isso faremos perceba que como estamos com uma divisão de polinômios, precisamos apenas igualar o numerador a zero, ou seja,
Sendo assim, é uma raiz para ,ou seja,
Logo, o gráfico de toca o eixo apenas uma vez.
Passo 3
Determinaremos agora e , para em seguida verificarmos se possui máximos, mínimos ou pontos de inflexão. Dessa maneira temos que,
Pela regra do quociente,
Calculando a segunda derivada utilizando a regra quociente e a regra da cadeia,
Passo 4
Vamos agora identificar se possui pontos críticos
Em relação aos pontos de inflexão temos que
Perceba que, para valores dentro do intervalo , assume valores positivos ( cresce). E para valores dentro do intervalo , irá assumir valores negativos (decresce). Logo, é um ponto de máximo no intervalo de
Passo 5
Vamos agora identificar se possui pontos de inflexão
Em relação aos pontos de inflexão temos que
No entanto, a raiz quadrada de um número negativo não existe nos reais. Sendo assim, não possui pontos críticos em seu domínio e consequentemente não tem mudança de concavidade
Passo 6
Para finalizar verificaremos se possui assíntotas verticais ou horizontais.
No que se refere as assíntotas horizontais temos que
Logo, possui uma assíntota horizontal em.
No que se refere as assíntotas verticais, perceba que apesar de não estar definida em , este ponto é uma assíntota vertical para , pois
Logo, possui assíntotas verticais em .
Resposta
