Se for uma função polinomial, mostre que entre duas raízes consecutivas da equação haverá no máximo uma raíz da equação .
Passo 1
Então galera, essa questão aqui é mais um raciocínio que envolvem os conceitos de máximos e mínimos. Uma das maneiras mais adequadas e intuitivas de se observar isso é graficamente. Se plotarmos o gráfico de uma função polinomial qualquer, galera, teremos algo desse tipo:
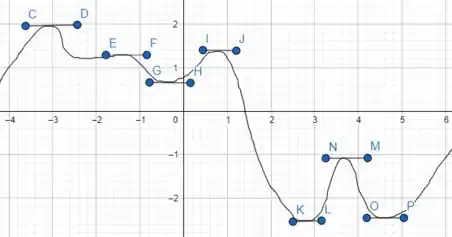
Mas po, o que são esses segmentos de reta aí? Então pessoal, esses são os pontos em que há máximos ou mínimos locais/relativos. A derivada de uma função não é dada por uma razão de taxa de variação? Se essa taxa de variação é zero em um determinado ponto, isto é, , isso implica que a reta tangente será horizontal, assim como representado na figura!
Passo 2
Uma vez compreendido o que são esses segmentos, vamos analisar esses pontos no qual com um pouco mais de profundidade. Galera, se a derivada em um ponto é zero, vocês concordam comigo que muito possivelmente (considerando que a função seja contínua) haverá mudança na concavidade do gráfico? A única forma de um gráfico passar de crescente para decrescente e vice-versa, é havendo um mínimo ou máximo relativo.
Vamos pegar dois segmentos de reta, assim como o enunciado solicita, ok? Pegaremos os segmentos e . Supondo que o nosso gráfico tocasse o eixo após passar pelo segmento , caracterizando uma raíz de ; seria completamente IMPOSSÍVEL haver mais de uma raíz de entre esses dois segmentos porque para o gráfico deixar de subir e começar a descer para poder passar novamente pelo eixo haveria uma inversão na concavidade do gráfico! Se há mudança de concavidade no gráfico, então já formaria outro ponto onde a derivada seria zero e ainda continuaria tendo apenas uma raíz entre e . Se representarmos isso graficamente, teríamos isso aqui ó:
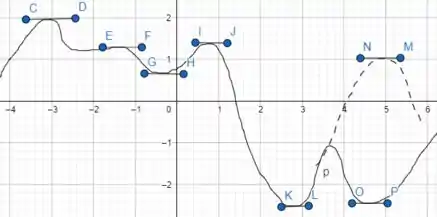
Supondo que o caminho a ser seguido fosse o pontilhado, note que para admitir outra raíz o gráfico teria que apresentar uma mudança de concavidade, o que já seria um outro ponto no qual . Sempre que forçamos para que essa situação ocorra, sempre volta no mesmo impasse: entre duas raízes de , sempre haverá, no máximo, uma raíz de .
Resposta
Ei, a resposta está no passo a passo :)