Exercícios de Concavidade - Lista de Exercícios Resolvida
Questão 1
O que se pode dizer sobre o gráfico de uma função que possui uma segunda derivada contínua que nunca é zero? Justifique sua resposta.
Ver solução completaQuestão 2
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Ver solução completaQuestão 3
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Ver solução completaQuestão 4
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Ver solução completaQuestão 5
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Ver solução completaQuestão 6
Em cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(d)
Ver solução completaQuestão 7
Em cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(c)
Ver solução completaQuestão 8
Seja duas vezes diferenciável tal que e para todo . Considere . No intervalo é correto afirmar que:
- é decrescente e côncava para baixo
- é crescente e côncava para baixo
- é decrescente e côncava para cima
- é crescente e côncava para cima
Questão 9
Disserte sobre como as derivadas afetam a forma de um gráfico. O seu texto deve responder as seguintes perguntas:
I. O que diz sobre ?
II. O que diz sobre ?
Ver solução completaQuestão 10
ME02) Considere as afirmações abaixo:
- Se uma função é côncava para cima então ela é necessariamente crescente em todo seu domínio
- O gráfico de uma função pode interceptar o eixo vertical mais de uma vez
Escolha a alternativa correta:
- Ambas são falsas
- Ambas são verdadeiras
- é falsa e é verdadeira
- é verdadeira e é falsa
Questão 11
Considere a função dada por:
É correto afirmar que tem concavidade pra baixo em:
Questão 13
- Seja a função , determine:
- Os intervalos onde a função tem concavidade voltada para cima e concavidade voltada para baixo e os pontos de inflexão.
Ver solução completaQuestão 14
Seja derivável em com . Considere as afirmativas abaixo:
- O gráfico de pode ser crescente com concavidade para baixo próximo de .
- O gráfico de pode ser decrescente com concavidade para cima próximo de .
É verdadeira ou são verdadeiras:
- As afirmativas (I) e (II).
- Nenhuma das afirmativas.
- Somente a afirmativa (I).
- Somente a afirmativa (II).
Questão 15
Seja . Admita que .
Estude a concavidade de e determine, caso existam, os pontos de inflexão;
Ver solução completaQuestão 16
Questão 2:
Considere a função
- Determine a primeira e a segunda derivada de .
- Determine as abscissas (coordenadas ) dos pontos de inflexão do gráfico de . Justifique sua resposta.
- Determine as ordenadas (coordenadas ) dos pontos de inflexão de .
Questão 17
Seja
- é crescente e seu gráfico é côncavo para cima quando .
- é decrescente e seu gráfico é côncavo para baixo quando .
- é crescente e seu gráfico é côncavo para baixo quando .
- é decrescente e seu gráfico é côncavo para baixo quando .
Questão 18
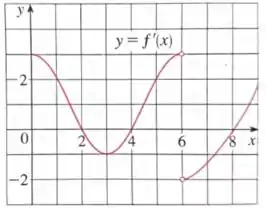
Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :
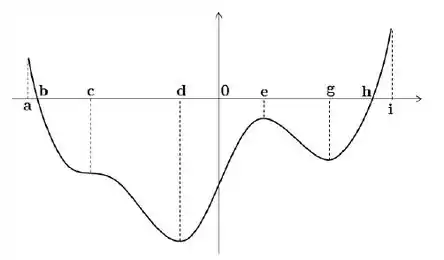
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta
d) No intervalo o gráfico de é côncavo pra cima
Ver solução completaQuestão 19
Considere a função dada por:
É correto afirmar que tem concavidade pra cima em:
Questão 20
Considere a função dada por:
É correto afirmar que tem concavidade pra baixo em:
Questão 21
Considere a função dada por:
É correto afirmar que tem concavidade pra cima em:
Questão 22
Dada a função , determine:
a concavidade e os pontos de inflexão de ;
Ver solução completaQuestão 24
Considere a função , definida em seu maior domínio possível.
d) Determine os intervalos onde tem concavidade para baixo e onde tem concavidade para cima. Determine também os pontos de inflexão, caso existam.
Ver solução completaQuestão 26
Considere a função cuja derivada é
(c) os intervalos onde o gráfico de tem concavidade para cima ou para baixo
Ver solução completaQuestão 27
Estude a função dada com relação à concavidade e pontos de inflexão:
b)
Ver solução completaQuestão 28
Estude a função dada com relação à concavidade e pontos de inflexão:
a)
Ver solução completaQuestão 29
Estude a função dada com relação à concavidade e pontos de inflexão:
e)
Ver solução completaQuestão 30
Estude a função dada com relação à concavidade e pontos de inflexão:
g)
Ver solução completaQuestão 31
Estude a função dada com relação à concavidade e pontos de inflexão:
i)
Ver solução completaQuestão 32
Estude a função dada com relação à concavidade e pontos de inflexão:
k)
Ver solução completaQuestão 33
Estude a função dada com relação à concavidade e pontos de inflexão:
j)
Ver solução completaQuestão 34
Estude a função dada com relação à concavidade e pontos de inflexão:
h)
Ver solução completaQuestão 35
Estude a função dada com relação à concavidade e pontos de inflexão:
f)
Ver solução completaQuestão 36
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
i)
- Determine os intervalos para os quais o gráfico de é côncavo para cima ou para baixo.
Questão 37
Estude a função dada com relação à concavidade e pontos de inflexão:
l)
Ver solução completaQuestão 38
Uma mosca está num arco de parábola . Descreva a parte desse arco no qual a mosca pode ficar a fim de não ser vista por um observador em .
Ver solução completaQuestão 39
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
e) Determine os intervalos para os quais o gráfico de é côncavo para cima ou para baixo.
Ver solução completaQuestão 40
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
g) Quais os pontos de inflexão do gráfico?
Ver solução completaQuestão 41
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Quais são os pontos de inflexão do gráfico?
Ver solução completaQuestão 42
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Determine os intervalos para os quais o gráfico de é côncavo para cima ou para baixo.
Ver solução completaQuestão 43
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Quais são os pontos de inflexão do gráfico?
Ver solução completaQuestão 44
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Determine os intervalos para os quais o gráfico de é côncavo para cima ou para baixo.
Ver solução completaQuestão 45
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Quais são os pontos de inflexão do gráfico?
Ver solução completaQuestão 46
- Considere a dada por e suas derivadas e
- Determine os intervalos nos quais o gráfico de é côncavo para cima e onde é côncavo para baixo.
Ver solução completaQuestão 48
Estude a função dada com relação à concavidade e pontos de inflexão:
d)
Ver solução completaQuestão 49
Estude a função dada com relação à concavidade e pontos de inflexão:
c)
Ver solução completaQuestão 50
Determine se as proposições abaixo são verdadeiras ou falsas, justificando suas respostas.
a) Se , então é ponto de inflexão do gráfico de .
b) Se , então .
Ver solução completaQuestão 51
Esboce, no espaço abaixo, o gráfico da função , determinando:
concavidades e pontos de inflexão, sabendo-se que ;
Ver solução completaQuestão 52
Seja Que condições devem satisfazer para que seja um ponto de inflexão?
Ver solução completaQuestão 54
Seja
(b) Determine os intervalos onde é côncava para cima/baixo e seus pontos de inflexão.
Ver solução completaQuestão 55
Seja
(b) Determine os intervalos onde é côncava para cima/baixo e seus pontos de inflexão.
Ver solução completaQuestão 56
Considere uma função duas vezes derivável e inversível.
Mostre que .
Considerando que é uma função decrescente cujo gráfico tem concavidade para cima, determine a concavidade do gráfico da .
Ver solução completaQuestão 59
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
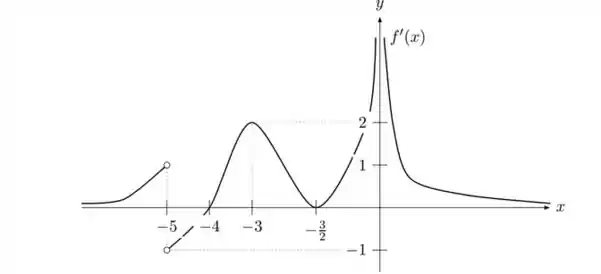
Responda, justificando, o que se pede:
os intervalos onde o gráfico de possui concavidade para cima e onde possui concavidade para baixo.
Ver solução completaQuestão 60
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
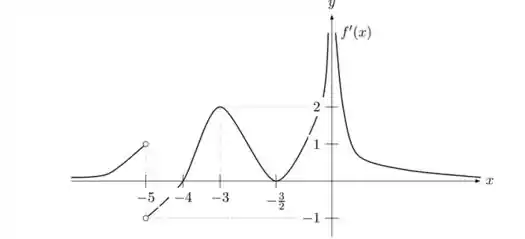
Responda, justificando, o que se pede:
os pontos de inflexão, caso existam;
Ver solução completaQuestão 61
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
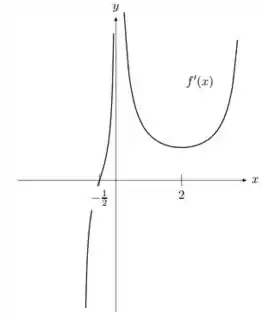
Responde o que se pede:
os intervalos onde o gráfico de possui concavidade para cima e onde possui concavidade para baixo.
Ver solução completaQuestão 62
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
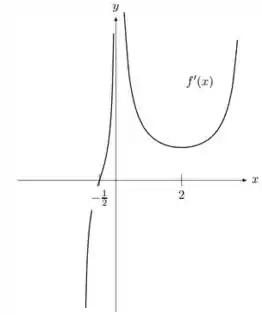
Responde o que se pede:
os pontos de inflexão, caso existam;
Ver solução completaQuestão 63
A entropia por partícula s de um gás ideal monoatômico é dada pela equação de Sackur-Tetrode:
onde u é a energia interna por partícula e v o volume total por partícula e k, m e h são constantes positivas. De acordo com a termodinâmica, s deve ver uma função côncava de suas variáveis, e uma forma de garantir isso é que se tenha e . Verifique se a função s dada satisfaz as condições acima, ou então indique quais relações entre as variáveis e constantes devem ser satisfeitas para que as condições de concavidade sejam válidas.
Ver solução completaQuestão 64
4) Considere a função , definida para . (Não precisa provar esse fato.)
a) Determine as assíntotas horizontais do gráfico de , ou justifique sua inexistência. Idem, considerando as assíntotas verticais.
b) Determine os intervalos de crescimento e decrescimento da função . Determine ainda os pontos de máximo e de mínimo de (se houver), indicando se são absolutos (globais) ou relativos (locais).
c) Determine os intervalos de concavidade para cima ou para baixo do gráfico de . Determine ainda os pontos de inflexão (se houver).
d) Usando as informações obtidas nos itens anteriores esboce o gráfico de . Deve incluir as assíntotas encontradas, e deve destacar os pontos notáveis obtidos junto com suas coordenadas.
Ver solução completaQuestão 65
Prove que se é um polinômio, a equação não pode ter infinitas soluções.
Ver solução completaQuestão 66
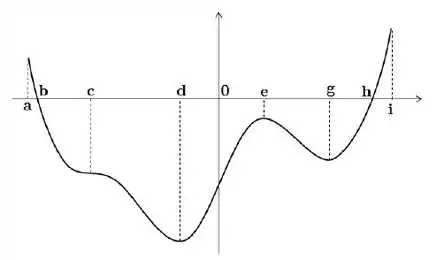
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
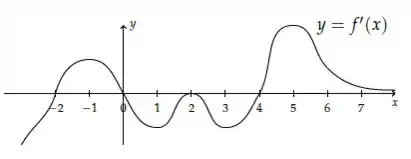
- Ache os pontos de inflexão de
Questão 67
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
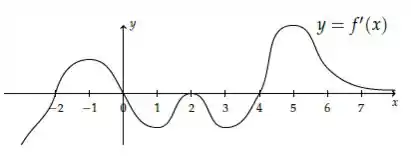
- Em que intervalos tem concavidade para cima ou para baixo?
Questão 68
Seja
(b) Determine os intervalos onde é côncava para cima/baixo e seus pontos de inflexão.
Ver solução completaQuestão 70
Dada a função , determine:
Intervalos das concavidades para cima e para baixo;
Ver solução completaQuestão 71
Em cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(b)
Ver solução completaQuestão 72
Em cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(a)
Ver solução completa