Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.2 - Ex. 3
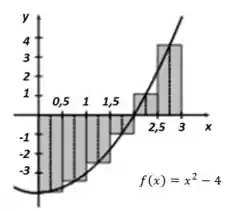
Se calcule a soma de Riemann com tomando como pontos amostrais os pontos médios. O que representa a soma de Riemann? Ilustre com um diagrama.
Passo 1
Fala aí pessoal, partiu resolver mais um problema de cálculo!!
Queremos calcular a soma de Riemann com no intervalo da seguinte função:
Lembrando que devemos adotar os pontos médios como pontos amostrais.
Tá.... mas o que é essa soma??
Bom... a soma de Riemann para uma função em um intervalo fechado com subintervalos é expressa como:
Onde:
- é um ponto amostral no -ésimo subintervalo;
- é a largura do -ésimo subintervalo .
Agora vamos aplicar!! 😉
Passo 2
O primeiro passo é calcular , que será:
Pegando o ponto médio:
Logo, separando o somatório da soma de Riemann para , temos:
Para ...
...
E assim por diante...
Substituindo:
Tranquilo até aqui?
Passo 3
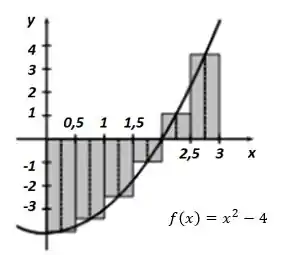
Essa soma representa a soma das áreas abaixo e acima do gráfico, utilizando a soma de retângulos. Representando isso, teremos:
Entendeu direitinho?? Responde Aí! 😉
Resposta
Essa soma representa a soma das áreas abaixo e acima do gráfico, utilizando a soma de retângulos. Representando isso, teremos:
