Funções da forma
onde é um inteiro positivo, surgem no estudo estatístico do fluxo de trânsito.
- Use um recurso gráfico para gerar o gráfico de com e e elabore uma conjectura sobre o número e a localização dos extremos relativos de .
- Confirme sua conjectura usando o teste da derivada primeira.
Passo 1
- Vamos esboçar os gráficos de com e e vamos analisar eles:
- Pronto, vamos lá, para achar os pontos relativos de vamos encontrar a primeira derivada:
Com :
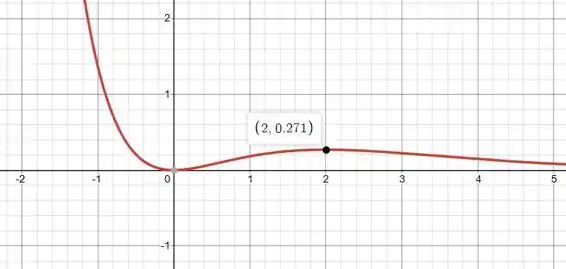
Com :
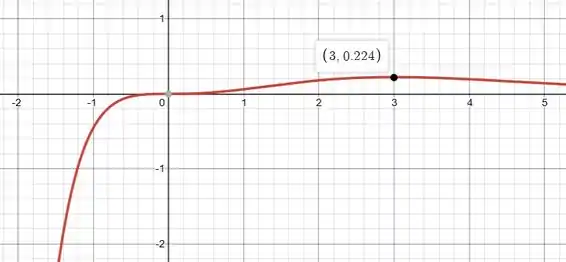
Com :
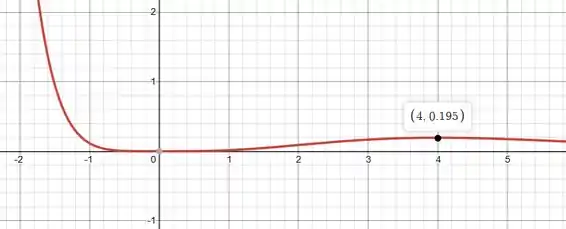
Com :
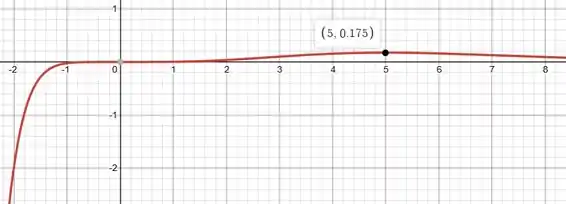
Pelos gráficos dá pra ver que tem um extremo relativo em cada valor de considerado, e eles são máximos relativos.
Passo 2
Agora fazendo vamos ver se possui algum ponto crítico, onde a derivada é zero, ou onde ela não existe:
Pronto, temos como pontos críticos então:
Passo 2
Agora vamos usar o Teste da Derivada Primeira:
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um máximo relativo em .
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um mínimo relativo em .
E se tiver o mesmo sinal tanto em um intervalo aberto imediatamente à esquerda de quanto em um intervalo aberto imediatamente à direita de , então não tem extremo relativo em .
Vamos então analisar as derivadas no intervalo com , :
Pronto, temos então que e , então tem um máximo relativo em , e isso vai acontecer para cada valor de .
Resposta
- Pelos gráficos dá pra ver que tem um extremo relativo em cada valor de considerado, e eles são máximos relativos.
- tem um máximo relativo em cada valor de , e isso vai acontecer para cada valor de .