Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 12
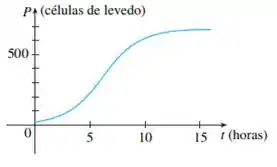
O gráfico mostrado corresponde ao da função população de cultura em laboratório de células de levedo. Use o método do Exemplo para obter o gráfico da derivada . O que o gráfico de nos diz sobre a população de levedos?
Passo 1
Fala galera! Prontos para resolver esse exercício?
Nele vamos treinar como esboçar o gráfico de uma derivada e interpretá-lo, tudo isso a partir do gráfico da função original.
Não vamos fazer nenhuma conta, só aplicar a teoria para ver se a gente ta entendendo tudo direitinho sobre o assunto!
Foi dado o gráfico de células de levedo em função do tempo
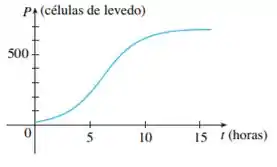
E usando o exemplo 1, temos que esboçar o gráfico de .
Tem ideia de como fazer isso?
O exemplo 1 usa uma estimativa da inclinação da reta tangente ao gráfico da função e a partir desses valores, esboça o gráfico da derivada.
Veja só!
Passo 2
Para desenhar o gráfico de , temos que ficar atentos a algumas características dao gráfico de . Primeiro: O gráfico de sempre está crescendo, logo, a derivada vai ser sempre positiva!
Para confirmar isso, primeiro vamos desenhar várias retas tangentes no gráfico:
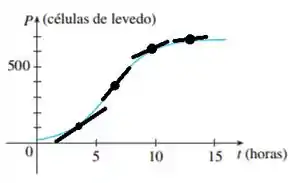
Perceba que as retas são crescentes ao longo do gráfico inteiro, logo, suas inclinações são positivas. Como a derivada nada mais é do que a inclinação da reta tangente à determinado ponto, confirmamos que a derivada é sempre positiva!
Além disso, podemos afirmar mais duas coisas: primeiro, que a máxima derivada ocorre mais ou menos no ponto (reta tangente mais inclindada) e, em segundo lugar, que a medida que o tempo passa, lá por volta de , a derivada vai se aproximando de zero (as retas tangentes vão ficando cada vez menos inclinadas).
Tranquilo até aqui?
Passo 3
Já analisamos o gráfico de , então podemos desenhar quem é ! Vamos ter um gráfico todo acima do eixo (valores de sempre positivos), que vai crescendo até atingir um pico quando . Depois, o gráfico vai caindo (as retas tangentes vão ficando menos inclinadas) até ficar bem pertinho do zero quando mais ou menos. Olha só como vai ficar o esboço então:
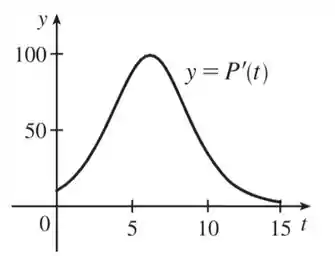
Bacana, não é?
Passo 4
Agora, precisamos analisar o que esse gráfico de significa! Se analisarmos qual será a unidade da derivada, teremos que ela será dada em . Ou seja: teremos o quão rápido o número de leveduras irá variar em cada hora!
A partir da conclusão que tiramos, podemos ver que o gráfico mostra a velocidade do crescimento populacional dessas leveduras. Elas vão crescendo rapidamente, sendo que a população aumenta a todo vapor lá por .
Depois disso, as leveduras vão se reproduzindo mais divagar, até que a população quase não cresce a partir de .
E aí! o que achou? Responde Aí!
Resposta
O esboço de vai ser:
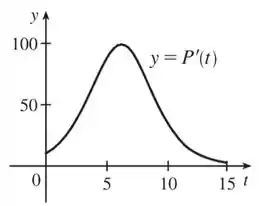
Podemos concluir que representa a velocidade do crescimento populacional das leveduras. A população vai crescendo cada vez mais rápido, atingindo seu auge de velocidade quando . Depois, ela vai crescendo cada vez mais devagar, se mantendo a um número quase que constante após .