a. Identifique os extremos locais de cada função nos intervalos dados e informe onde eles ocorrem.

b. Na mesma tela, esboce os gráficos da função e de sua derivada. Comente o comportamento de f em relação aos sinais e valores de .

Para achar os pontos críticos, vamos igualar a derivada a zero.

Achamos o nossos pontos críticos.

Vamos fazer nossa análise de sinal dentro do nosso intervalo:

E temos que: ; ;

Então temos pontos de máximo local quando e ponto de mínimo local quando , em que a função vale -3.

b) Gráficos:

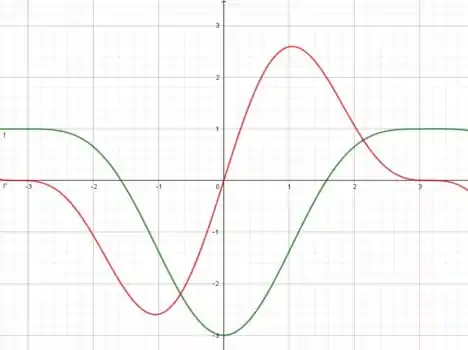
Vemos que quando , a função é decrescente, e quando a função é crescente, e também vemos o ponto de mínimo em x=0.