Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 7c

Inverta a ordem de integração.

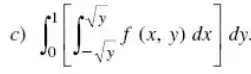
Passo 1

Para realizar a inversão, o primeiro passo é descobrir a região de integração e o conjunto B . Assim, visto que y varia de 0 a 1 , para cada valor de y fixo em [ 0 , 1 ] , x varia de - sqrt(y) a sqrt(y) . Logo, conclui-se que essa região é o conjunto:

B = {(x , y) in R^2 | 0 <= y <= 1 , - sqrt(y) <= x <= sqrt(y)}

Passo 2

Esboçando esse conjunto obtém-se:

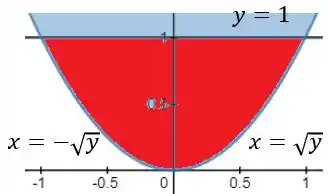
Assim, ao inverter a ordem de integração e reescrevendo as inequações, deixando y em função de x , resulta em:

y >= x^2

Passo 3

Portanto, invertendo a ordem de integração temos:

int_0^1 [int_(- sqrt(y))^(sqrt(y)) f (x , y) d x] d y = int_(- 1)^1 [int_(x^2)^1 f (x , y) d y] d x

Resposta

int_(- 1)^1 [int_(x^2)^1 f (x , y) d y] d x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 1 3 ∫ 1 x d yd x